题目内容

11．如图所示的长方形阴影区域的面积是（　　）
A．9B．12C．14D．16

分析 根据长方形在坐标平面内得到其宽和高，由面积公式可得．

解答 解：由图形可知该矩形的宽为4-1=3，高为4，
则长方形的面积为3×4=12，
故选：B．

点评 本题主要考查坐标与图形的面积，根据图形在坐标平面内的位置得到其宽和高是解题的关键．

练习册系列答案
相关题目
2．若一元二次方程2x2-（a+1）x=x（x-1）-1化成一般形式后，二次项系数与一次项系数互为相反数．则a的值为（　　）
A．-1B．1C．-2D．2
19．如图，图中可以只用一个大写字母表示的角有（　　）
A．1个B．2个C．3个D．4个
6．已知两点A（-5，y1），B（3，y2）均在抛物线y=ax2+bx+c（a≠0）上，点C（x0，y0）是该抛物线的顶点．若y1＜y2≤y0，则x0的取值范围是（　　）
A．-5≤x0-3B．-5≤x0＜2C．x0≥-5D．-5≤x0＜-1
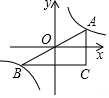16．如图，过原点O的直线交双曲线y=$\frac{k}{x}$于A、B两点，分别过A、B向两坐标轴作垂线相交于点C，若△ABC的面积是12，则k=（　　）
A．4B．6C．8D．12
3．对于二项方程axn+b=0（a≠0，b≠0），当n为偶数时，已知方程无实数根，那么ab一定（　　）
A．ab＜0B．ab≤0C．ab＞0D．ab≥0
20．已知关于x、y的二元一次方程组$\left\{\begin{array}{l}2x-5y=2k-3\\ x+3y=5k\end{array}\right.$．
（1）求方程组的解；（用含k的代数式表示）；
（2）若-1＜k≤1，设S=x-8y，求S的取值范围．
1．解下列方程：
（1）5（x-5）-2（12-x）=0
（2）$\frac{2x+1}{4}$-1=x-$\frac{10x+1}{12}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网