题目内容
某种商品的成本是120元,试销阶段每件商品的售价x(元)与产品的销售量y(件)满足当x=130时,y=70,当x=150时,y=50,且y是x的一次函数,为了获得最大利润S(元),每件产品的销售价应定为( )
| A、160元 | B、180元 |
| C、140元 | D、200元 |
考点:二次函数的应用
专题:
分析:把x=130时,y=70,当x=150时,y=50,代入一函数解析式y=kx+b,进而得出y与x的关系式;利用利润=销量×每件利润,进而利用配方法求出函数最值.
解答:解:设y=kx+b,将(130,70),(150,50)代入得:
即
,
解得:
,
∴y与x之间的一次函数关系式为:y=-x+200;
销售利润为S,由题意得:
S=(x-120)y
=-x2+320x-24000
=-(x-160)2+1600,
∴售价为160元/件时,获最大利润1600元.
故选:A.
即
|
解得:
|
∴y与x之间的一次函数关系式为:y=-x+200;
销售利润为S,由题意得:
S=(x-120)y
=-x2+320x-24000
=-(x-160)2+1600,
∴售价为160元/件时,获最大利润1600元.
故选:A.
点评:此题主要考查了二次函数的应用,利用配方法求出函数最值是解题关键.

练习册系列答案
相关题目
下列函数中,y的值随着x逐渐增大而减小的是( )
| A、y=2x | ||
| B、y=x2 | ||
C、y=-
| ||
D、y=
|
 有理数a、b在数轴上对应点如图,则下列说法错误的是( )
有理数a、b在数轴上对应点如图,则下列说法错误的是( )| A、|a|>|b| |
| B、a>b |
| C、a、b中正数绝对值大 |
| D、a与b互为相反数 |
下列说法正确的是( )
| A、某工厂质检员检测某批灯泡的使用寿命采用普查法 |
| B、一组数据1,a,4,4,9的平均数是4,则这组数据的方差是7.6 |
| C、12名同学中有两人的出生月份相同是必然事件 |
| D、一组数据:5,4,3,6,4中,中位数是3 |
 如图,CA交⊙O于点D,AB为⊙O直径,点E是弧ABD上异于点A、D的一点,若∠E=38°,则∠BAC的度数为
如图,CA交⊙O于点D,AB为⊙O直径,点E是弧ABD上异于点A、D的一点,若∠E=38°,则∠BAC的度数为 已知:如图,AC=DF,AC∥DF,AE=DB.求证:①△ABC≌△DEF;②BC∥EF.
已知:如图,AC=DF,AC∥DF,AE=DB.求证:①△ABC≌△DEF;②BC∥EF.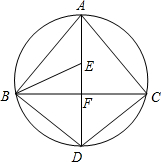 如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为点F,∠ABC的平分线AD于点E,连接BD,CD.
如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为点F,∠ABC的平分线AD于点E,连接BD,CD.