题目内容
16.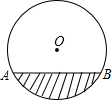 如图,是一圆柱形输水管的横截面,阴影部分为有水部分,如果水面宽8cm,水的最大深度为2cm,求该输水管的半径是多少?
如图,是一圆柱形输水管的横截面,阴影部分为有水部分,如果水面宽8cm,水的最大深度为2cm,求该输水管的半径是多少?
分析 先过点O作OD⊥AB于点D,连接OA,由垂径定理可知AD=$\frac{1}{2}$AB,设OA=r,则OD=r-2,在Rt△AOD中,利用勾股定理即可求出r的值.
解答 解:过点O做OC⊥AB于点D,连接OA.
设半径长为rcm,
∵OC⊥AB,
∴AD=$\frac{1}{2}$AB
=$\frac{1}{2}$×8
=4(cm),
∵CD=2cm∴OD=r-2(cm)
在Rt△AOD中,由勾股定理得:(r-2)2+42=r2
r2-4r+4+42=42
4r=20
r=5,
答:该水管的半径是5cm.
点评 本题考查的是垂径定理的应用及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
7.“十一”黄金周期间,某风景区在7天假期中每天旅游的人数变化如表:(正数表示比前一天多的人数,负数表示比前一天少的人数)(单位:万人),已知9月30日游客为2万.
(1)求10月2日游客的人数为多少?
(2)请判断7天内游客人数最多的是哪天?最少的是哪天?它们相差多少万人?
(3)求这一次黄金周期间游客在该地的总人数.
| 日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
| 人数变化 | +1.6 | +0.8 | +0.4 | -0.4 | -0.8 | +0.2 | -1.2 |
(2)请判断7天内游客人数最多的是哪天?最少的是哪天?它们相差多少万人?
(3)求这一次黄金周期间游客在该地的总人数.
8.数轴上表示整数的点称为整点.某数轴上的单位长度是1cm,若在这个数轴上随意画出一条长2016cm的线段AB,则线段AB盖住的整点个数是( )
| A. | 2017个或2018个 | B. | 2016个或2017个 | C. | 2015个或2016个 | D. | 2014个或2015个 |
5.函数y=-$\frac{1}{4}$(2x-1)2+1的二次项系数为( )
| A. | -$\frac{1}{4}$ | B. | -$\frac{1}{2}$ | C. | -1 | D. | 1 |
6. 把一张长方形的纸条按如图所示那样折叠后,若量得∠AOB′=40°,则∠B′OG的度数为( )
把一张长方形的纸条按如图所示那样折叠后,若量得∠AOB′=40°,则∠B′OG的度数为( )
 把一张长方形的纸条按如图所示那样折叠后,若量得∠AOB′=40°,则∠B′OG的度数为( )
把一张长方形的纸条按如图所示那样折叠后,若量得∠AOB′=40°,则∠B′OG的度数为( )| A. | 40° | B. | 70° | C. | 60° | D. | 80° |
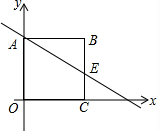 如图,正方形ABCD的边长是2,E是BC的中点.
如图,正方形ABCD的边长是2,E是BC的中点.