题目内容
18.若a,b均为整数,a+b=-2,且a≥2b,则$\frac{a}{b}$有最大值1.分析 分别求出a、b的取值范围,然后求出$\frac{a}{b}$的最大值.
解答 解:a=-2-b,
-2-b≥2b,
解得:b≤-$\frac{2}{3}$,
b=-2-a,
a≥-4-2a,
解得:a≥-$\frac{4}{3}$,
∵a,b均为整数,
∴当a=-1,b=-1时,
$\frac{a}{b}$有最大值1.
故答案为:1.
点评 本题考查了解一元一次不等式,解不等式要依据不等式的基本性质:
(1)不等式的两边同时加上或减去同一个数或整式不等号的方向不变;
(2)不等式的两边同时乘以或除以同一个正数不等号的方向不变;
(3)不等式的两边同时乘以或除以同一个负数不等号的方向改变.

练习册系列答案
相关题目
9. 在开会前,工作人员进行会场布置,如图为工作人员在主席台上由两人拉着一条绳子,然后以“准绳”摆放整齐的茶杯,这样做的理由是( )
在开会前,工作人员进行会场布置,如图为工作人员在主席台上由两人拉着一条绳子,然后以“准绳”摆放整齐的茶杯,这样做的理由是( )
 在开会前,工作人员进行会场布置,如图为工作人员在主席台上由两人拉着一条绳子,然后以“准绳”摆放整齐的茶杯,这样做的理由是( )
在开会前,工作人员进行会场布置,如图为工作人员在主席台上由两人拉着一条绳子,然后以“准绳”摆放整齐的茶杯,这样做的理由是( )| A. | 两点之间线段最短 | B. | 两点确定一条直线 | ||
| C. | 垂线段最短 | D. | 过一点可以作无数条直线 |
 已知:如图,点O是直线AB上一点,过点O作射线OC,使∠AOC=120°.
已知:如图,点O是直线AB上一点,过点O作射线OC,使∠AOC=120°.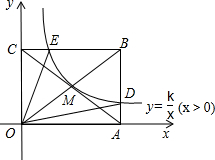 如图,反比例函数$y=\frac{k}{x}({x>0})$的图象经过矩形OABC对角线的交点M,分别与AB、BC相交于点D、E,若四边形ODBE的面积为12,则k的值为4.
如图,反比例函数$y=\frac{k}{x}({x>0})$的图象经过矩形OABC对角线的交点M,分别与AB、BC相交于点D、E,若四边形ODBE的面积为12,则k的值为4.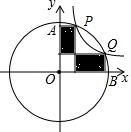 如图,点P(2,6)是函数y=$\frac{k}{x}$(k≠0)图象上的一点,以OP为半径作扇形OAB,交y轴于点A,交x轴于点B,且与函数y=$\frac{k}{x}$(k≠0)图象交于点Q.从点P,Q分别向x轴,y轴作垂线,则图中阴影部分的面积是16.
如图,点P(2,6)是函数y=$\frac{k}{x}$(k≠0)图象上的一点,以OP为半径作扇形OAB,交y轴于点A,交x轴于点B,且与函数y=$\frac{k}{x}$(k≠0)图象交于点Q.从点P,Q分别向x轴,y轴作垂线,则图中阴影部分的面积是16.