题目内容
3.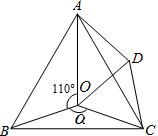 如图,点O是等边△ABC内一点,∠AOB=100°,∠BOC=α,D是△ABC外一点,且△BOC≌△ADC,连接OD.
如图,点O是等边△ABC内一点,∠AOB=100°,∠BOC=α,D是△ABC外一点,且△BOC≌△ADC,连接OD.(1)△COD是什么三角形?说明理由;
(2)当α为多少度时,△AOD是直角三角形?
(3)当α为多少度时,△AOD是等腰三角形?
分析 (1)根据全等三角形的性质得到CO=CD,∠BCO=∠ACD,由等边三角形的性质得到∠ACB=60°,求得∠OCD=∠ACB=60°;即可得到结论;
(2)根据等边三角形的性质和周角的定义解答即可;
(3)分三种情况::①要使AO=AD,需∠AOD=∠ADO,根据周角的定义得到∠ADO=α-60°,得到方程190°-α=α-60°求得α=125°;②要使OA=OD,需∠OAD=∠ADO.由于∠AOD=190°-α,∠ADO=α-60°,于是得到α-60°=50°求得α=110°;③要使OD=AD,需∠OAD=∠AOD.由于190°-α=50°于是得到α=140°.
解答 解:(1)△COD是等边三角形,理由如下:
∵△BOC≌△ADC,
∴CO=CD,∠BCO=∠ACD,
∵△ABC是等边三角形,
∴∠ACB=60°,
∴∠OCD=∠ACB=60°;
∴△COD是等边三角形;
(2)∵△COD是等边三角形,
∴∠COD=60°,
∵△AOD是直角三角形,
∴∠AOD=90°,
∴∠α=360°-110°-90°-60°=100°;
(3)①要使AO=AD,需∠AOD=∠ADO.
∵∠AOD=360°-∠AOB-∠COD-α=360°-100°-60°-α=200°-α,∠ADO=α-60°,
∴200°-α=α-60°
∴α=130°;
②要使OA=OD,需∠OAD=∠ADO.
∵∠AOD=200°-α,∠ADO=α-60°,
∴∠OAD=180°-(∠AOD+∠ADO)=40°,
∴α-60°=40°
∴α=100°;
③要使OD=AD,需∠OAD=∠AOD.
∵200°-α=40°
∴α=160°,
当α=150°时,△AOD也是直角三角形.
综上所述:当α的度数为130°,或100°,150°或160°时,△AOD是等腰三角形
点评 本题考查了全等三角形的性质,等边三角形的性质,勾股定理的逆定理,等腰三角形的判定,熟练掌握全等三角形的性质定理是解题的关键.

 (答案要求保留小数点后两位数)已知一次考试中某题得分的频数分布表
(答案要求保留小数点后两位数)已知一次考试中某题得分的频数分布表| 得分 | 0分 | 1分 | 2分 | 3分 | 4分 | 5分 | 合计 |
| 频数 | 2 | 4 | 6 | 16 | 8 | 6 | 42 |
| 频率 | 0.05 | 0.10 | 0.14 | 0.38 | 0.19 | 0.14 | 1 |
(2)该题的平均得分是3;得3分的人数最多,占总人数的38%;
(3)将该题的得分情况制作成扇形统计图.
| A. | AB=A′B′,AC=A′C,∠B=∠B′ | B. | AB=A′B′,BC=B′C,∠A=∠A′ | ||
| C. | AC=A′C′,BC=B′C′,∠C=∠C′ | D. | AC=A′C′,BC=B′C′,∠B=∠B′ |
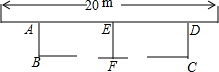 如图,利用一面墙(墙的长度为20m),用34m长的篱笆围成两个鸡场,中间用一道篱笆隔开,每个鸡场均留一道1m宽的门,设AB的长为x米.若两个鸡场总面积为96m2,求x.
如图,利用一面墙(墙的长度为20m),用34m长的篱笆围成两个鸡场,中间用一道篱笆隔开,每个鸡场均留一道1m宽的门,设AB的长为x米.若两个鸡场总面积为96m2,求x. 如图:在△ABC中,DE∥BC,交AB于D,交AC于E,且AB=16cm,AC=12cm,BC=20cm.
如图:在△ABC中,DE∥BC,交AB于D,交AC于E,且AB=16cm,AC=12cm,BC=20cm.