题目内容
14.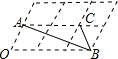 如图,6个形状、大小完全相同的菱形组成网格,菱形的顶点称为格点.已知菱形的一个角(∠O)为60°,A,B,C都在格点上,则tan∠ABC的值是$\frac{\sqrt{3}}{2}$.
如图,6个形状、大小完全相同的菱形组成网格,菱形的顶点称为格点.已知菱形的一个角(∠O)为60°,A,B,C都在格点上,则tan∠ABC的值是$\frac{\sqrt{3}}{2}$.
分析 如图,连接EA、EB,先证明∠AEB=90°,根据tan∠ABC=$\frac{AE}{EB}$,求出AE、EB即可解决问题.
解答 解:如图,连接EA,EC,设菱形的边长为a,由题意得∠AEF=30°,∠BEF=60°,AE=$\sqrt{3}$a,EB=2a
∴∠AEC=90°,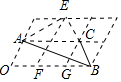
∵∠ACE=∠ACG=∠BCG=60°,
∴E、C、B共线,
在Rt△AEB中,tan∠ABC=$\frac{AE}{BE}$=$\frac{\sqrt{3}a}{2a}$=$\frac{\sqrt{3}}{2}$.
故答案为$\frac{\sqrt{3}}{2}$.
点评 本题考查菱形的性质,三角函数、特殊三角形边角关系等知识,解题的关键是添加辅助线构造直角三角形解决问题,属于中考常考题型.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
4.羊年除夕当日微信红包收发总量达80.8亿个.其中80.8亿用科学记数法可表示为( )
| A. | 8.08×108 | B. | 0.808×109 | C. | 8.08×109 | D. | 0.808×1010 |
2. 如图,直线a,b被直线c所截,∠1与∠2的位置关系是( )
如图,直线a,b被直线c所截,∠1与∠2的位置关系是( )
 如图,直线a,b被直线c所截,∠1与∠2的位置关系是( )
如图,直线a,b被直线c所截,∠1与∠2的位置关系是( )| A. | 同位角 | B. | 内错角 | C. | 同旁内角 | D. | 对顶角 |
9.下表是某校合唱团成员的年龄分布
对于不同的x,下列关于年龄的统计量不会发生改变的是( )
| 年龄/岁 | 13 | 14 | 15 | 16 |
| 频数 | 5 | 15 | x | 10-x |
| A. | 平均数、中位数 | B. | 众数、中位数 | C. | 平均数、方差 | D. | 中位数、方差 |
3.宁波栎社国际机场三期扩建工程建设总投资84.5亿元,其中84.5亿元用科学记数法表示为( )
| A. | 0.845×1010元 | B. | 84.5×108元 | C. | 8.45×109元 | D. | 8.45×1010元 |


 从一个边长为3cm的大立方体挖去一个边长为1cm的小立方体,得到的几何体如图所示,则该几何体的左视图正确的是( )
从一个边长为3cm的大立方体挖去一个边长为1cm的小立方体,得到的几何体如图所示,则该几何体的左视图正确的是( )



