题目内容
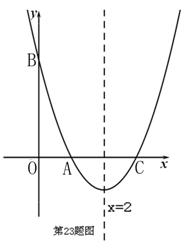
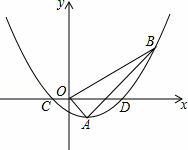
如图,在平面直角坐标系中,顶点为A(1,﹣1)的抛物线经过点B(5,3),且与x轴交于C,D两点(点C在点D的左侧).
(1)求抛物线的解析式;
(2)求点O到直线AB的 距离;
距离;
(3)点M在第二象限内的抛物线上,点N在x轴上,且∠MND=∠OAB,当△DMN与△OAB相似时,请你直接写出点M的坐标.
解:(1)设抛物线的解析式为y=a(x﹣1)2﹣1,
将B点坐标代入函数解析式,得
(5﹣1)2a﹣1=3,
解得a= .
.
故抛物线的解析式为y= (x﹣1)2﹣1;
(x﹣1)2﹣1;
(2)由勾股定理,得OA2=11+12=2,OB2=52+32=34,AB2=(5﹣1)2+(3+1)2=32,
OA2+AB2=OB2,
∴∠OAB=90°,
O到直线AB的距离是OA= ;
;
(3)设M(a,b),N(a,0)
当y=0时, (x﹣1)2﹣1=0,
(x﹣1)2﹣1=0,
解得x1=3,x2=﹣1,
D(3,0),DN=3﹣a.
①当△MND∽△OAB时, =
= ,即
,即 =
= ,
,
化简,得4b=a﹣3 ①
M在抛物线上,得b= (a﹣1)2﹣1 ②
(a﹣1)2﹣1 ②
联立①②,得 ,
,
解得a1=3(不符合题意,舍),a2=﹣2,b= ,
,
M1(﹣2, ),
),
当△MND∽△BAO时, =
= ,即
,即 =
= ,
,
化简,得b=12﹣4a ③,
联立②③,得 ,
,
解得a1=3(不符合题意,舍),a2=﹣17,b=1 2﹣4×(﹣17)=80,
2﹣4×(﹣17)=80,
M2(﹣17,80).
综上所述:当△DMN与△OAB相似时,点M的坐标(﹣2, ),(﹣17,80).
),(﹣17,80).

练习册系列答案
相关题目
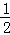
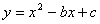 交
交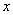 轴于点A(1,0),交
轴于点A(1,0),交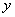 轴于点B,对称轴是
轴于点B,对称轴是