题目内容
如果x-y=
+1,y-z=
-1,那么x2+y2+z2-xy-yz-zx= .
| 2 |
| 2 |
考点:完全平方公式
专题:计算题
分析:根据已知的两个等式,相加可得x-z=2
③,再求①2+②2+③2的值,整理化简即可求x2+y2+z2-xy-yz-yx的值.
| 2 |
解答:解:∵x-y=
+1①,y-z=
-1②,
∴x-z=2
③,
则①2+②2+③2=(x-y)2+(y-z)2+(x-z)2=(
+1)2+(
-1)2+(2
)2=14,
即2(x2+y2+z2-xy-yz-yx)=14,
∴x2+y2+z2-xy-yz-yx=7.
故答案为:7.
| 2 |
| 2 |
∴x-z=2
| 2 |
则①2+②2+③2=(x-y)2+(y-z)2+(x-z)2=(
| 2 |
| 2 |
| 2 |
即2(x2+y2+z2-xy-yz-yx)=14,
∴x2+y2+z2-xy-yz-yx=7.
故答案为:7.
点评:本题主要考查完全平方公式.完全平方公式:(a±b)2=a2±2ab+b2.

练习册系列答案
相关题目
若-
≤x≤1,则式子
+
+
等于( )
| 1 |
| 2 |
| x2-2x+1 |
| x2-6x+9 |
| 4x2+4x+1 |
| A、-4x+3 | B、5 |
| C、2x+3 | D、4x+3 |
若
-
=1,则代数式
的值( )
| x |
| 2 |
| y |
| 3 |
| 9x+y-18 |
| 9x-y-18 |
A、等于
| ||
B、等于
| ||
C、等于
| ||
D、等于
|
不超过(
+
)6的最大整数是( )
| 7 |
| 3 |
| A、7038 | B、7039 |
| C、7040 | D、7041 |
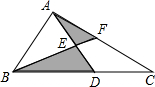 如图,△ABC的面积等于25cm2,AE=ED,BD=2DC.则△AEF与△BDE的面积之和等于
如图,△ABC的面积等于25cm2,AE=ED,BD=2DC.则△AEF与△BDE的面积之和等于