题目内容
8．
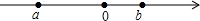实数a，b在数轴上的位置如图所示，且|a|＞|b|，则化简$\sqrt{{a}^{2}}$-|2a+b|的结果为（ ）| A． | 2a+b | B． | -2a+b | C． | a+b | D． | 2a-b |
分析 首先根据实数a，b在数轴上的位置，可得a＜0＜b；然后分别求出$\sqrt{{a}^{2}}$、|2a+b|的值各是多少，再把所得结果相减，求出化简$\sqrt{{a}^{2}}$-|2a+b|的结果为多少即可．
解答 解：根据图示，可得a＜0＜b，
∴$\sqrt{{a}^{2}}$-|2a+b|=（-a）-（-2a-b）=-a+2a+b=a+b．
故选：C．
点评 （1）此题主要考查了实数与数轴问题，要熟练掌握，解答此题的关键是判断出：a＜0＜b．
（2）此题还考查了一个数的算术平方根和绝对值的求法，要熟练掌握．
练习册系列答案
相关题目
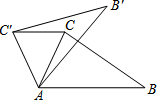如图，将△ABC绕点A逆时针旋转40°到△AB′C′的位置，则∠ACC′=70°．
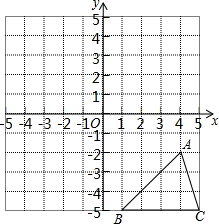在平面直角坐标系中，按照下列要求作图：
已知有理数a、b、c在数轴上的位置如图所示，且|a|=|b|．化简：|a|-|a+b|-|c-a|+|ac|-|-2b|．