题目内容
9.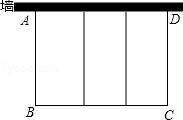 如图,孔明想利用一面长为45米的墙建羊圈,用100米的围栏围成总面积为600平方米的三个大小相同的矩形羊圈,求羊圈的边长AB,BC各为多少米?孔明能在原来的基础上建一个面积为640平方米的羊圈吗?说说理由.
如图,孔明想利用一面长为45米的墙建羊圈,用100米的围栏围成总面积为600平方米的三个大小相同的矩形羊圈,求羊圈的边长AB,BC各为多少米?孔明能在原来的基础上建一个面积为640平方米的羊圈吗?说说理由.
分析 (1)设AB的长度为x米,则BC的长度为(100-4x)米;然后根据矩形的面积公式列出方程求解即可;
(2)设AB=y米,则BC=(100-4y)米,根据羊圈的面积为640平方米列出方程y(100-4y)=640,即y2-25y+160=0,由△=(-25)2-4×160<0,可得孔明不能在原来的基础上建一个面积为640平方米的羊圈.
解答 解:(1)设AB=x米,则BC=(100-4x)米,根据题意得:
x(100-4x)=640,
解得:x1=10,x2=15.
①当AB=10时,BC=60(不合题意舍去);
②当AB=15时,BC=40符合题意;
答:羊圈的边长AB,BC分别是20米、20米;
(2)不能.
理由:设AB=y米,则BC=(100-4y)米,根据题意得:
y(100-4y)=640,
整理得:y2-25y+160=0,
∵△=(-25)2-4×160<0,
∴孔明不能在原来的基础上建一个面积为640平方米的羊圈.
点评 本题考查了一元二次方程的应用.解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.

练习册系列答案
相关题目
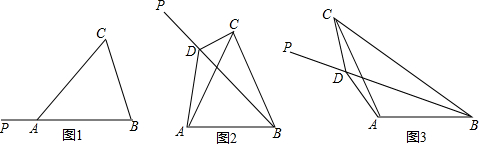
14.如图①,在△ABC中,∠ACB=90°,∠CAB=30°,△ABD是等边三角形.如图②,将四边形ACBD折叠,使D与C重合,EF为折痕,则∠ACE的正弦值为( )
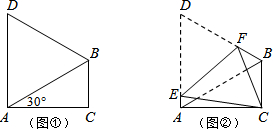

| A. | $\frac{\sqrt{3}-1}{7}$ | B. | $\frac{1}{7}$ | C. | $\frac{\sqrt{3}}{12}$ | D. | $\frac{\sqrt{3}-1}{6}$ |
1.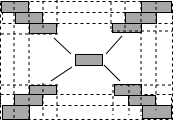 如图,某广场的休闲区由1×1的小正方形瓷砖无空隙地铺成长方形,若该休闲区黑色小正方形共有82块,则白色小正方形的块数是( )
如图,某广场的休闲区由1×1的小正方形瓷砖无空隙地铺成长方形,若该休闲区黑色小正方形共有82块,则白色小正方形的块数是( )
 如图,某广场的休闲区由1×1的小正方形瓷砖无空隙地铺成长方形,若该休闲区黑色小正方形共有82块,则白色小正方形的块数是( )
如图,某广场的休闲区由1×1的小正方形瓷砖无空隙地铺成长方形,若该休闲区黑色小正方形共有82块,则白色小正方形的块数是( )| A. | 340 | B. | 380 | C. | 402 | D. | 424 |
18.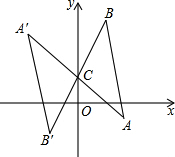 如图,将△ABC绕点C(0,1)旋转180°得到△A′B′C,设点A′的坐标为(a,b),则点A的坐标为( )
如图,将△ABC绕点C(0,1)旋转180°得到△A′B′C,设点A′的坐标为(a,b),则点A的坐标为( )
 如图,将△ABC绕点C(0,1)旋转180°得到△A′B′C,设点A′的坐标为(a,b),则点A的坐标为( )
如图,将△ABC绕点C(0,1)旋转180°得到△A′B′C,设点A′的坐标为(a,b),则点A的坐标为( )| A. | (-a,-b) | B. | (-a,-b+2) | C. | (-a,-b+1) | D. | (-a,-b-1) |
19.若反比例函数y=$\frac{k}{x}$的图象经过点(2,-6),则k的值为( )
| A. | -12 | B. | 12 | C. | -3 | D. | 3 |
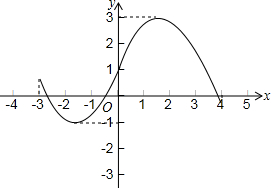 若y是关于x的函数,H是常数(H>0),若对于此函数图象上的任一两点(x1,y1),(x2,y2),都有|y1-y2|≤H,则称该函数为有界函数,其中满足条件的所有常数H的最小值,称为该函数的界高.
若y是关于x的函数,H是常数(H>0),若对于此函数图象上的任一两点(x1,y1),(x2,y2),都有|y1-y2|≤H,则称该函数为有界函数,其中满足条件的所有常数H的最小值,称为该函数的界高.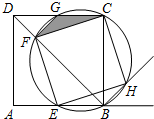 如图,点E是边长为1的正方形ABCD的边AB上任意一点(不含A、B),过B、C、E三点的圆与BD相交于点F,与CD相交于点G,与∠ABC的外角平分线相交于点H.
如图,点E是边长为1的正方形ABCD的边AB上任意一点(不含A、B),过B、C、E三点的圆与BD相交于点F,与CD相交于点G,与∠ABC的外角平分线相交于点H.