题目内容
20.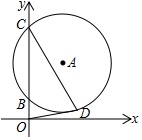 如图,以点A(1,$\sqrt{3}$)为圆心的⊙A交y轴正半轴于B、C两点,且OC=$\sqrt{3}$+1,点D是⊙A上第一象限内的一点,连接OD、CD.若OD与⊙A相切,则CD的长为( )
如图,以点A(1,$\sqrt{3}$)为圆心的⊙A交y轴正半轴于B、C两点,且OC=$\sqrt{3}$+1,点D是⊙A上第一象限内的一点,连接OD、CD.若OD与⊙A相切,则CD的长为( )| A. | $\sqrt{3}$-1 | B. | $\sqrt{3}$+1 | C. | 2$\sqrt{3}$ | D. | 2$\sqrt{2}$ |
分析 连接OA,连接AC,过点A作AE⊥OC于E,过点D作DF⊥CF交CA的延长线于F.首先证明△AOD为等腰直角三角形,在Rt△ADF,Rt△CDF中,解直角三角形即可解决问题.
解答 解:连接OA,连接AC,过点A作AE⊥OC于E,过点D作DF⊥CF交CA的延长线于F.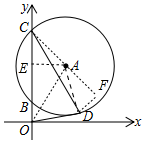
∵A(1,$\sqrt{3}$),
∴OA=$\sqrt{{1}^{2}+(\sqrt{3})^{2}}$=2,
∴CE=AE=1,AC=AD=$\sqrt{2}$
∴OD=$\sqrt{2}$,
∵AD=OD,∠ADO=90°,
∴△AOD为等腰直角三角形,
∴∠DAF=180°-45°-60°-45°=30°,
∴DF=$\frac{\sqrt{2}}{2}$,AF=$\frac{\sqrt{6}}{2}$,CF=$\sqrt{2}$+$\frac{\sqrt{6}}{2}$,
在Rt△CDF中,CD=$\sqrt{C{F}^{2}+D{F}^{2}}$=$\sqrt{(\sqrt{2}+\frac{\sqrt{6}}{2})^{2}+(\frac{\sqrt{2}}{2})^{2}}$=$\sqrt{3}$+1.
故选B.
点评 本题考查切线的性质、坐标与图形的性质、等腰直角三角形的判定和性质、30度的直角三角形的性质等知识,解题的关键是学会填空常用辅助线,构造特殊三角形解决问题,属于中考常考题型.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
5.下列各组数中,不是互为相反意义的量的是( )
| A. | 向东走20千米与向西走15千米 | B. | 收入200元与亏损30元 | ||
| C. | 超过0.05mm与不足0.03mm | D. | 上升10米和下降7米 |
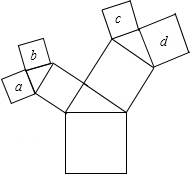 在如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,若最大正方形的边长为7cm,则正方形a,b,c,d的面积之和是147cm2.
在如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,若最大正方形的边长为7cm,则正方形a,b,c,d的面积之和是147cm2.