题目内容
14.快递员小林某天下午用三轮摩托在东西走向的一条大街上送快递,若规定向东为正,向西为负,则他这天下午行车里程(单位:km)可表示如下:+7.5,-1.5,+7,-5.5,+5,-6,+3,-7.5,+8,-9
(1)将最后一件快递送到目的时,小林离出发点距离多少千米?
(2)已知三轮摩托耗油为每1千米0.4元,求该车这天下午的油费.
分析 (1)根据有理数的加法运算,算得所有数据的和,根据和的绝对值,可得答案;
(2)所有数据绝对值的和,再乘1千米耗油的费用即可得出答案.
解答 解:(1)7.5-1.5+7-5.5+5-6+3-7.5+8-9=1(千米)
答:最后一件快递送到目的时,小林离出发点距离1千米;
(2)(|+7.5|+|-1.5|+|+7|+|-5.5|+|+5|+|-6|+|+3|+|-7.5|+|+8|+|-9|)×0.4
=60×0.4
=24(元)
答:这天下午油费24元.
点评 本题考查了正数和负数,理解题意,正确列式,运用有理数的加法运算法则计算是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.8个$\frac{3}{8}$的和是( )
| A. | $\frac{8}{3}$ | B. | $\frac{3}{2}$ | C. | 3 | D. | $\frac{1}{16}$ |
19.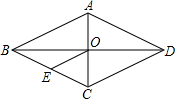 已知:如图,菱形ABCD中,对角线AC与BD相交于点O,E是BC中点E,AD=6cm,则OE的长为( )
已知:如图,菱形ABCD中,对角线AC与BD相交于点O,E是BC中点E,AD=6cm,则OE的长为( )
 已知:如图,菱形ABCD中,对角线AC与BD相交于点O,E是BC中点E,AD=6cm,则OE的长为( )
已知:如图,菱形ABCD中,对角线AC与BD相交于点O,E是BC中点E,AD=6cm,则OE的长为( )| A. | 6cm | B. | 4cm | C. | 3cm | D. | 2cm |
3.已知二次函数y=kx2-7x-7的图象和x轴有交点,则k的取值范围是( )
| A. | k>-$\frac{7}{4}$ | B. | k≥-$\frac{7}{4}$ | C. | k≥-$\frac{7}{4}$且k≠0 | D. | k>-$\frac{7}{4}$且k≠0 |
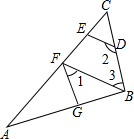 如图,DE⊥AC,∠AGF=∠ABC,∠1+∠2=180°.
如图,DE⊥AC,∠AGF=∠ABC,∠1+∠2=180°. 如图,在△ABC中,AD⊥DC,∠BAD=30°,∠BCD=18°,则∠B=42°.
如图,在△ABC中,AD⊥DC,∠BAD=30°,∠BCD=18°,则∠B=42°.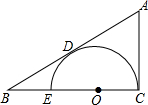 已知如图:在△ABC中,∠ACB=Rt∠,⊙O的O点在BC上,且AB切⊙O于D,若OC:CB=1:3,AD=4.求BE的长.
已知如图:在△ABC中,∠ACB=Rt∠,⊙O的O点在BC上,且AB切⊙O于D,若OC:CB=1:3,AD=4.求BE的长.