题目内容
9. 如图,在△ABC中,AD⊥DC,∠BAD=30°,∠BCD=18°,则∠B=42°.
如图,在△ABC中,AD⊥DC,∠BAD=30°,∠BCD=18°,则∠B=42°.
分析 先在△ADC中利用三角形内角和得到∠DAC+∠DCA=90°,则可计算出∠BAC+∠BCA=138°,然后在△ABC中利用三角形内角和求∠B的度数.
解答 解:∵AD⊥DC,
∴∠ADC=90°,
∴∠DAC+∠DCA=90°,
∴∠BAC+∠BCA=∠BAD+∠DAC+∠DCA+∠BCD=30°+90°+18°=138°,
∴∠B=180°-(∠BAC+∠BCA)=180°-138°=42°.
故答案为42°.
点评 本题考查了三角形内角和定理:三角形内角和是180°.三角形内角和主要用在求三角形中角的度数.

练习册系列答案
相关题目
17.已知点(-4,y1),(2,y2)都在直线y=-2x+1上,则y1,y2的大小关系是( )
| A. | y1>y2 | B. | y1<y2 | C. | y1=y2 | D. | 不能比较 |
19.一元二次方程x2-x-1=0的两个实数根中较大的根是( )
| A. | 1+$\sqrt{5}$ | B. | $\frac{1+\sqrt{5}}{2}$ | C. | $\frac{1-\sqrt{5}}{2}$ | D. | $\frac{-1+\sqrt{5}}{2}$ |
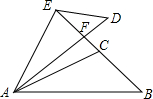 如图所示,△ABC≌△ADE,BC的延长线过点E,∠ACB=∠AED=105°,∠CAD=10°,∠B=50°,∠DEF的度数是35°.
如图所示,△ABC≌△ADE,BC的延长线过点E,∠ACB=∠AED=105°,∠CAD=10°,∠B=50°,∠DEF的度数是35°.