题目内容
4.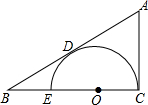 已知如图:在△ABC中,∠ACB=Rt∠,⊙O的O点在BC上,且AB切⊙O于D,若OC:CB=1:3,AD=4.求BE的长.
已知如图:在△ABC中,∠ACB=Rt∠,⊙O的O点在BC上,且AB切⊙O于D,若OC:CB=1:3,AD=4.求BE的长.
分析 连结OD,如图,设⊙O的半径为r,则OC=OD=r,OB=2r,根据切线的性质得∠BDO=90°,则利用正弦的定义可求出∠B=30°,再判断AC为⊙O的切线,根据切线长定理可得AC=AD=4,然后在Rt△ABC中,利用正切定义可计算出BC=4$\sqrt{3}$,于是可得BE=OE=$\frac{4\sqrt{3}}{3}$.
解答 解:连结OD,如图,设⊙O的半径为r,则OC=OD=r,OB=2r,
∵AB切⊙O于D,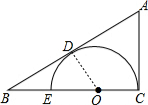
∴OD⊥AB,
∴∠BDO=90°,
在Rt△BOD中,∵sinB=$\frac{OD}{OB}$=$\frac{r}{2r}$=$\frac{1}{2}$,
∴∠B=30°,
∵∠ACB=90°,
∴AC为⊙O的切线,
∴AC=AD=4,
在Rt△ABC中,∵tanB=$\frac{AC}{BC}$,
∴BC=$\frac{4}{tan30°}$=4$\sqrt{3}$,
∴r=$\frac{4\sqrt{3}}{3}$,
∴BE=OE=$\frac{4\sqrt{3}}{3}$.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了解直角三角形.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
15.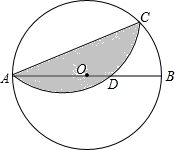 如图,⊙O中,弦AC=$\sqrt{15}$,沿AC折叠劣弧$\widehat{AC}$交直径AB于D,DB=$\frac{1}{2}$,则直径AB=( )
如图,⊙O中,弦AC=$\sqrt{15}$,沿AC折叠劣弧$\widehat{AC}$交直径AB于D,DB=$\frac{1}{2}$,则直径AB=( )
 如图,⊙O中,弦AC=$\sqrt{15}$,沿AC折叠劣弧$\widehat{AC}$交直径AB于D,DB=$\frac{1}{2}$,则直径AB=( )
如图,⊙O中,弦AC=$\sqrt{15}$,沿AC折叠劣弧$\widehat{AC}$交直径AB于D,DB=$\frac{1}{2}$,则直径AB=( )| A. | 4 | B. | $\frac{15}{4}$ | C. | 3$\sqrt{2}$ | D. | 2$\sqrt{5}$ |
19.一元二次方程x2-x-1=0的两个实数根中较大的根是( )
| A. | 1+$\sqrt{5}$ | B. | $\frac{1+\sqrt{5}}{2}$ | C. | $\frac{1-\sqrt{5}}{2}$ | D. | $\frac{-1+\sqrt{5}}{2}$ |
9.数a与3的和的2倍,可列代数式为( )
| A. | 2(a+3) | B. | 2a+3 | C. | 3a+2 | D. | 3(a+2) |
