题目内容
如图,已知第一象限内的图象是反比例函数 图象的一个分支,第二象限内的图象是反比例函数
图象的一个分支,第二象限内的图象是反比例函数 图象的一个分支,在x轴的上方有一条平行于x轴的直线l与它们分别交于点A、B,过点A、B作x轴的垂线,垂足分别为C、D.若四边形ABCD的周长为8且AB<AC,则点A的坐标为 .
图象的一个分支,在x轴的上方有一条平行于x轴的直线l与它们分别交于点A、B,过点A、B作x轴的垂线,垂足分别为C、D.若四边形ABCD的周长为8且AB<AC,则点A的坐标为 .

( ,3).
,3).
【解析】
试题分析:设A点坐标为(a, ),利用AB平行于x轴,点B的纵坐标为
),利用AB平行于x轴,点B的纵坐标为 ,而点B在反比例函数y=-
,而点B在反比例函数y=- 图象上,易得B点坐标为(-2a,
图象上,易得B点坐标为(-2a, ),则AB=a-(-2a)=3a,AC=
),则AB=a-(-2a)=3a,AC= ,然后根据矩形的性质得到AB+AC=4,即3a+
,然后根据矩形的性质得到AB+AC=4,即3a+ =4,则3a2-4a+1=0,用因式分解法解得a1=
=4,则3a2-4a+1=0,用因式分解法解得a1= ,a2=1,而AB<AC,则a=
,a2=1,而AB<AC,则a= ,即可写出A点坐标.
,即可写出A点坐标.
试题解析:点A在反比例函数 图象上,设A点坐标为(a,
图象上,设A点坐标为(a, ),
),
∵AB平行于x轴,
∴点B的纵坐标为 ,
,
而点B在反比例函数y=- 图象上,
图象上,
∴B点的横坐标=-2×a=-2a,即B点坐标为(-2a, ),
),
∴AB=a-(-2a)=3a,AC= ,
,
∵四边形ABCD的周长为8,而四边形ABCD为矩形,
∴AB+AC=4,即3a+ =4,
=4,
整理得,3a2-4a+1=0,(3a-1)(a-1)=0,
∴a1= ,a2=1,
,a2=1,
而AB<AC,
∴a= ,
,
∴A点坐标为( ,3).
,3).
考点:反比例函数综合题.

练习册系列答案
相关题目

 +mx +5 =0是一元二次方程.
+mx +5 =0是一元二次方程. ,则 AC=( )
,则 AC=( )

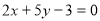 ,求
,求 的值.
的值.