题目内容
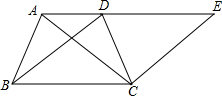 如图,等腰梯形ABCD中,AB=DC,对角线AC=BD,AD∥BC,点E是AD延长线上一点,∠E=∠DBC.
如图,等腰梯形ABCD中,AB=DC,对角线AC=BD,AD∥BC,点E是AD延长线上一点,∠E=∠DBC.(1)试说明:DE=BC;
(2)试判断△ACE的形状,并说明理由.
考点:等腰梯形的性质
专题:
分析:(1)根据AD∥BC,得到∠BCD=∠CDE,又因为DE=BC,所以△BCD≌△EDC,根据全等三角形的对应边相等即可求得结论;
(2)根据全等三角形对应边相等得到BD=CE,又因为等腰梯形的对角线相等,所以AC=CE,所以是等腰三角形.
(2)根据全等三角形对应边相等得到BD=CE,又因为等腰梯形的对角线相等,所以AC=CE,所以是等腰三角形.
解答:解:(1)∵AD∥BC,
∴AE∥BC,
∴∠BCD=∠EDC.
在△BCD和△EDC中,
,
∴△BCD≌△EDC(AAS)
∴DE=BC;
(2)△ACE是等腰三角形.
∵△BCD≌△EDC,
∴BD=CE,
∵AC=BD,
∴AC=CE,
∴△ACE是等腰三角形.
∴AE∥BC,
∴∠BCD=∠EDC.
在△BCD和△EDC中,
|
∴△BCD≌△EDC(AAS)
∴DE=BC;
(2)△ACE是等腰三角形.
∵△BCD≌△EDC,
∴BD=CE,
∵AC=BD,
∴AC=CE,
∴△ACE是等腰三角形.
点评:本题主要考查等腰梯形的性质和全等三角形的判定,利用全等三角形的对应边相等是常用的方法之一,同学们要注意理清解题思路.

练习册系列答案
相关题目
 如图,甲船从A港出发,沿北偏东60°方向航行1000m到达C港,乙船从B港出发,沿西北方向航行2000m到达C港,则S△ABC=
如图,甲船从A港出发,沿北偏东60°方向航行1000m到达C港,乙船从B港出发,沿西北方向航行2000m到达C港,则S△ABC=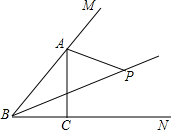 如图,点P为∠ABC和∠MAC的平分线的交点.求证:点P在∠ACN的平分线上.
如图,点P为∠ABC和∠MAC的平分线的交点.求证:点P在∠ACN的平分线上.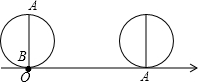 王老师在讲“实数”这节时,做了如下实验:如图所示,AB是半径为1的圆的直径,将B点放在数轴的原点上,将圆沿数轴向右滚动,A点刚好落在数轴上时,A点对应的数为
王老师在讲“实数”这节时,做了如下实验:如图所示,AB是半径为1的圆的直径,将B点放在数轴的原点上,将圆沿数轴向右滚动,A点刚好落在数轴上时,A点对应的数为 如图是一均匀薄板,半径R=30cm,现从板上挖掉一个r=15cm的内切圆,试求剩余薄板的重心C与大圆圆心O的距离.
如图是一均匀薄板,半径R=30cm,现从板上挖掉一个r=15cm的内切圆,试求剩余薄板的重心C与大圆圆心O的距离.