题目内容
微山湖花圃用花盆培育某种花卉,经市场调查发现,出售一盆花的盈利与该盆中花的棵树有关,当每盆栽种3棵时,平均每棵盈利3元,以同样的栽培条件,每盆增加1棵,平均每棵盈利将减少0.5元.设每盆增加种植花卉x棵,每盆盈利y 元.
元.
(1)写出y(元)与x(棵)之间的函数关系式;
(2)要使每盆盈利达到10元,每盆应当种植该种花卉多少棵?
【考点】一元二次方程的应用;二次函数的应用.
【专题】销售问题.
【分析】(1)根据题意可知:每盆花苗有(x+3)株,得出平均单株盈利为(3﹣0.5x)元,由此得出每盆盈利y=(x+3)(3﹣0.5x)即可;
(2)由题意得(x+3)(3﹣0.5x)=10进一步解方程求出即可.
【解答】解:(1)如果每盆花苗(假设原来花盆中有3株)增加x株,则每盆花苗有(x+3)株,平均单株盈利为3﹣0.5x元,
则每盆盈利y=(x+3)(3﹣0.5x);
(2)由题意得:(x+3)(3﹣0.5x)=10.
化简,整理,的x2﹣3x+2=0.
解这个方程,得x1=1,x2=2,
则3+1=4,2+3=5,
答:每盆应植4株或者5株.
【点评】此题考查了一元二次方程的应用,二次函数的运用,找出数量关系每盆花苗株数×平均单株盈利=总盈利是解题关键.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
 ﹣(﹣2.75)+(﹣5
﹣(﹣2.75)+(﹣5 )
) 两个正方形边长都是1,那么圆形纸片和扇形纸片的面积比是( )
两个正方形边长都是1,那么圆形纸片和扇形纸片的面积比是( )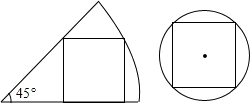
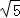 :2 D.
:2 D.
 _____元;这种篮球每月的销售量是__________个;(用含x的代数式表示)
_____元;这种篮球每月的销售量是__________个;(用含x的代数式表示)