题目内容
11．解分式方程：（1）$\frac{2}{x+2}=\frac{3}{x-2}$
（2）$\frac{x}{x-1}$-1=$\frac{3}{（x-1）（x+2）}$．
分析 两分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．
解答 解：（1）去分母得：2x-4=3x+6，
解得：x=-10，
经检验x=-10是分式方程的解；
（2）去分母得：x（x+2）-（x-1）（x+2）=3，
去括号得：x2+2x-x2-x+2=3，
解得：x=1，
经检验x=1是增根，分式方程无解．
点评 此题考查了解分式方程，解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．解分式方程一定注意要验根．
练习册系列答案
相关题目
19．
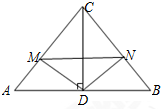如图，在Rt△ABC中，∠ACB=90°，AC=BC，CD⊥AB，M、N是AC、BC上的动点，且∠MDN=90°，下列结论正确的有（ ）个
（1）AM=CN；（2）S四边形MDNC是定值；
（3）AM2+BN2=MN2；（4）MN平分∠CND．
如图，在Rt△ABC中，∠ACB=90°，AC=BC，CD⊥AB，M、N是AC、BC上的动点，且∠MDN=90°，下列结论正确的有（ ）个（1）AM=CN；（2）S四边形MDNC是定值；
（3）AM2+BN2=MN2；（4）MN平分∠CND．
| A． | 4个 | B． | 3个 | C． | 2个 | D． | 1个 |
如图，直线AB与CD相交于点D，且∠AOC+∠BOD=140°，则∠AOD等于110°．
如图，直线a，b被直线c所截，现给出下列四个条件：①∠1=∠5；②∠4=∠6；③∠4+∠5=180°；④∠3+∠8=180°．其中能判定a∥b的条件的个数有（ ）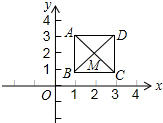
如图，已知正方形ABCD，顶点A（1，3）、B（1，1）、C（3，1）．规定“把正方形ABCD先沿x轴翻折，再向左平移1个单位”为一次变换，如此这样，连续经过2015次变换后，正方形ABCD的对角线交点M的坐标变为（-2013，-2）．