题目内容
9. 如图,在矩形ABCD中,BC=6,CD=3,将△BCD沿对角线BD翻折,点C落在点C′处,BC′交AD于点E,则线段DE的长为( )
如图,在矩形ABCD中,BC=6,CD=3,将△BCD沿对角线BD翻折,点C落在点C′处,BC′交AD于点E,则线段DE的长为( )| A. | 3 | B. | $\frac{15}{4}$ | C. | 5 | D. | $\frac{15}{2}$ |
分析 首先根据题意得到BE=DE,然后根据勾股定理得到关于线段AB、AE、BE的方程,解方程即可解决问题.
解答 解:设ED=x,则AE=6-x,
∵四边形ABCD为矩形,
∴AD∥BC,
∴∠EDB=∠DBC;
由题意得:∠EBD=∠DBC,
∴∠EDB=∠EBD,
∴EB=ED=x;
由勾股定理得:
BE2=AB2+AE2,
即x2=9+(6-x)2,
解得:x=3.75,
∴ED=3.75.
故选:B.
点评 本题主要考查了几何变换中的翻折变换及其应用问题;解题的关键是根据翻折变换的性质,结合全等三角形的判定及其性质、勾股定理等几何知识,灵活进行判断、分析、推理或解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19. 如图,在直角坐标系中,有两点A(6,3),B(6,0),以原点O位似中心,相似比为$\frac{1}{3}$,在第一象限内把线段AB缩小后得到线段CD,则点C的坐标为( )
如图,在直角坐标系中,有两点A(6,3),B(6,0),以原点O位似中心,相似比为$\frac{1}{3}$,在第一象限内把线段AB缩小后得到线段CD,则点C的坐标为( )
 如图,在直角坐标系中,有两点A(6,3),B(6,0),以原点O位似中心,相似比为$\frac{1}{3}$,在第一象限内把线段AB缩小后得到线段CD,则点C的坐标为( )
如图,在直角坐标系中,有两点A(6,3),B(6,0),以原点O位似中心,相似比为$\frac{1}{3}$,在第一象限内把线段AB缩小后得到线段CD,则点C的坐标为( )| A. | (2,1) | B. | (2,0) | C. | (3,3) | D. | (3,1) |
 如图,△ABC中,AB=AC,AD⊥BC,CE⊥AB,AE=CE.求证:
如图,△ABC中,AB=AC,AD⊥BC,CE⊥AB,AE=CE.求证: 如图,已知Rt△ABC中,∠ACB=90°,AC=6,BC=4,将△ABC绕直角顶点C顺时针旋转90°得到△DEC.若点F是DE的中点,连接AF,则AF=5.
如图,已知Rt△ABC中,∠ACB=90°,AC=6,BC=4,将△ABC绕直角顶点C顺时针旋转90°得到△DEC.若点F是DE的中点,连接AF,则AF=5.



 如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,交AB于点E,过点D作DF⊥AB,垂足为F,连接DE.
如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,交AB于点E,过点D作DF⊥AB,垂足为F,连接DE.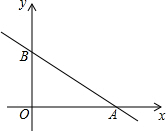 如图,已知直线y=-$\frac{3}{4}$x+3分别与x,y轴交于点A和B.
如图,已知直线y=-$\frac{3}{4}$x+3分别与x,y轴交于点A和B.