题目内容
 已知:直角坐标系xoy中,将直线y=kx沿y轴向下平移3个单位长度后恰好经过B(-3,0)及y轴上的C点.若抛物线y=-x2+bx+c与x轴交于A,B两点(点A在点B的右侧),且经过点C,
已知:直角坐标系xoy中,将直线y=kx沿y轴向下平移3个单位长度后恰好经过B(-3,0)及y轴上的C点.若抛物线y=-x2+bx+c与x轴交于A,B两点(点A在点B的右侧),且经过点C,(1)求直线BC及抛物线的解析式;
(2)设抛物线的顶点为D,点P在抛物线的对称轴上,且∠APD=∠ACB,求点P的坐标.
分析:(1)先根据y=kx沿y轴向下平移3个单位长度后经过y轴上的点C求出C点的坐标,再用待定系数法求出直线BC的解析式,再根据抛物线y=-x2+bx+c过点B,C,把B、C两点的坐标代入所设函数解析式即可求出此解析式;
(2)根据(1)中二次函数的解析式可求出A、D两点的坐标,判断出△OBC是等腰直角三角形,利用锐角三角函数的定义可求出∠OBC的度数,过点A作AE⊥BC于点E,利用勾股定理可求出BE、AE及CE的长,再根据相似三角形的判定定理可得出△AEC∽△AFP,根据相似三角形的对应边成比例可求出PF的长,再点P在抛物线的对称轴上即可求出点P的坐标.
(2)根据(1)中二次函数的解析式可求出A、D两点的坐标,判断出△OBC是等腰直角三角形,利用锐角三角函数的定义可求出∠OBC的度数,过点A作AE⊥BC于点E,利用勾股定理可求出BE、AE及CE的长,再根据相似三角形的判定定理可得出△AEC∽△AFP,根据相似三角形的对应边成比例可求出PF的长,再点P在抛物线的对称轴上即可求出点P的坐标.
解答: 解:(1)∵y=kx沿y轴向下平移3个单位长度后经过y轴上的点C,
解:(1)∵y=kx沿y轴向下平移3个单位长度后经过y轴上的点C,
∴此时直线的解析式为y=kx-3,令x=0,则y=-3,
∴C(0,-3)(1分)
设直线BC的解析式为y=kx-3.(1分)
∵B(-3,0)在直线BC上,
∴-3k-3=0解得k=-1.
∴直线BC的解析式为y=-x-3.(1分)
∵抛物线y=-x2+bx+c过点B,C,
∴
(2分)
解得
,
∴抛物线的解析式为y=-x2-4x-3;(1分)
(2)由y=-x2-4x-3.可得D(-2,1),A(-1,0).(1分)
∴OB=3,OC=3,OA=1,AB=2,
可得△OBC是等腰直角三角形.
∴∠OBC=45°,CB=3
.(1分)
设抛物线对称轴与x轴交于点F,
∴AF=
AB=1.
过点A作AE⊥BC于点E.
∴∠AEB=90°.
可得BE=AE=
,CE=2
,(1分)
在△AEC与△AFP中,∠AEC=∠AFP=90°,∠ACE=∠APF,
∴△AEC∽△AFP.(1分)
∴
=
,
=
,
解得,PF=2,
∵点P在抛物线的对称轴上,
∴点P的坐标为(-2,-2),(-2,2).(2分)
 解:(1)∵y=kx沿y轴向下平移3个单位长度后经过y轴上的点C,
解:(1)∵y=kx沿y轴向下平移3个单位长度后经过y轴上的点C,∴此时直线的解析式为y=kx-3,令x=0,则y=-3,
∴C(0,-3)(1分)
设直线BC的解析式为y=kx-3.(1分)
∵B(-3,0)在直线BC上,
∴-3k-3=0解得k=-1.
∴直线BC的解析式为y=-x-3.(1分)
∵抛物线y=-x2+bx+c过点B,C,
∴
|
解得
|
∴抛物线的解析式为y=-x2-4x-3;(1分)
(2)由y=-x2-4x-3.可得D(-2,1),A(-1,0).(1分)
∴OB=3,OC=3,OA=1,AB=2,
可得△OBC是等腰直角三角形.
∴∠OBC=45°,CB=3
| 2 |
设抛物线对称轴与x轴交于点F,
∴AF=
| 1 |
| 2 |
过点A作AE⊥BC于点E.
∴∠AEB=90°.
可得BE=AE=
| 2 |
| 2 |
在△AEC与△AFP中,∠AEC=∠AFP=90°,∠ACE=∠APF,
∴△AEC∽△AFP.(1分)
∴
| AE |
| AF |
| CE |
| PF |
| ||
| 1 |
2
| ||
| PF |
解得,PF=2,
∵点P在抛物线的对称轴上,
∴点P的坐标为(-2,-2),(-2,2).(2分)
点评:本题考查的是二次函数综合题,涉及到用待定系数法求一次函数及二次函数的解析式、等腰直角三角形的判定与性质、特殊角度的三角函数值及相似三角形的判定与性质,涉及面较广,难度较大.

练习册系列答案
相关题目
 要求写自变量的取值范围);
要求写自变量的取值范围); .折叠后,点O落在点O1,点C落在线段AB点C1处,并且DO1与DC1在同一直线上.
.折叠后,点O落在点O1,点C落在线段AB点C1处,并且DO1与DC1在同一直线上.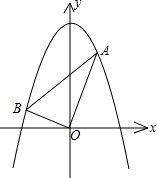 接OA,OB,OA⊥OB.
接OA,OB,OA⊥OB. A,OB,OA⊥OB
A,OB,OA⊥OB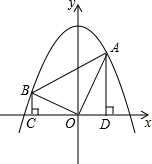 A,OB,OA⊥OB,作BC⊥x轴于C点,AD⊥x轴于D点.
A,OB,OA⊥OB,作BC⊥x轴于C点,AD⊥x轴于D点.