题目内容
如图,已知平面直角坐标系xOy中,点A(m,6),B(n,1)为两动点,其中0<m<3,连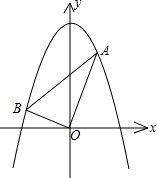 接OA,OB,OA⊥OB.
接OA,OB,OA⊥OB.(1)求证:mn=-6;
(2)当S△AOB=10时,抛物线经过A,B两点且以y轴为对称轴,求抛物线对应的二次函数的关系式;
(3)在(2)的条件下,设直线AB交y轴于点F,过点F作直线l交抛物线于P,Q两点,问是否存在直线l,使S△POF:S△QOF=1:3?若存在,求出直线l对应的函数关系式;若不存在,请说明理由.
分析:(1)作BC⊥x轴于C点,AD⊥x轴于D点,证明△CBO∽△DOA,利用线段比求出mn.
(2)由(1)得OA=mBO推出
OB•OA=10,根据勾股定理求出mn的值.然后可得A,B的坐标以及抛物线解析式.
(3)假设存在直线l交抛物线于P、Q两点,使PF:PQ=1:3,作PM⊥y轴于M点,QN⊥y轴于N点,设P坐标为(x,-x2+10),证明△PMF∽△QNF推出x值,继而可解出点P、Q的坐标.
(2)由(1)得OA=mBO推出
| 1 |
| 2 |
(3)假设存在直线l交抛物线于P、Q两点,使PF:PQ=1:3,作PM⊥y轴于M点,QN⊥y轴于N点,设P坐标为(x,-x2+10),证明△PMF∽△QNF推出x值,继而可解出点P、Q的坐标.
解答: (1)证明:作BC⊥x轴于C点,AD⊥x轴于D点,
(1)证明:作BC⊥x轴于C点,AD⊥x轴于D点,
∵A,B点坐标分别为(m,6),(n,1),
∴BC=1,OC=-n,OD=m,AD=6,
又OA⊥OB,
易证△CBO∽△DOA,
∴
=
,
∴
=
∴mn=-6.
(2)解:由(1)得,∵△CBO∽△DOA,
∴
=
=
,即OA=mBO,
又∵S△AOB=10,
∴
OB•OA=10,
即OB•OA=20,
∴mBO2=20,
又OB2=BC2+OC2=n2+1,
∴m(n2+1)=20,
∵mn=-6,
∴m=2,n=-3,
∴A坐标为(2,6),B坐标为(-3,1),易得抛物线解析式为y=-x2+10.
(3)解:直AB为y=x+4,且与y轴交于F(0,4)点,
∴OF=4,
假设存在直线l交抛物线于P,Q两点,且使S△POF:S△QOF=1:3,如图所示,
则有PF:FQ=1:3,作PM⊥y轴于M点,QN⊥y轴于N点,
∵P在抛物线y=-x2+10上,
∴设P坐标为(x,-x2+10),
则FM=OM-OF=(-x2+10)-4=-x2+6,
易证△PMF∽△QNF,
∴
=
=
=
,
∴QN=3PM=-3x,NF=3MF=-3x2+18,
∴ON=-3x2+14,
∴Q点坐标为(-3x,3x2-14),
∵Q点在抛物线y=-x2+10上,
∴3x2-14=-9x2+10,
解得:x=-
,
∴P坐标为(-
,8),Q坐标为(3
,-8),
∴易得直线PQ为y=2
x+4.
根据抛物线的对称性可得直线PQ另解为y=-2
x+4.
 (1)证明:作BC⊥x轴于C点,AD⊥x轴于D点,
(1)证明:作BC⊥x轴于C点,AD⊥x轴于D点,∵A,B点坐标分别为(m,6),(n,1),
∴BC=1,OC=-n,OD=m,AD=6,
又OA⊥OB,
易证△CBO∽△DOA,
∴
| CB |
| CO |
| DO |
| DA |
∴
| 1 |
| m |
| -n |
| 6 |
∴mn=-6.
(2)解:由(1)得,∵△CBO∽△DOA,
∴
| OB |
| OA |
| BC |
| OD |
| 1 |
| m |
又∵S△AOB=10,
∴
| 1 |
| 2 |
即OB•OA=20,
∴mBO2=20,
又OB2=BC2+OC2=n2+1,
∴m(n2+1)=20,
∵mn=-6,
∴m=2,n=-3,
∴A坐标为(2,6),B坐标为(-3,1),易得抛物线解析式为y=-x2+10.
(3)解:直AB为y=x+4,且与y轴交于F(0,4)点,
∴OF=4,
假设存在直线l交抛物线于P,Q两点,且使S△POF:S△QOF=1:3,如图所示,
则有PF:FQ=1:3,作PM⊥y轴于M点,QN⊥y轴于N点,
∵P在抛物线y=-x2+10上,
∴设P坐标为(x,-x2+10),
则FM=OM-OF=(-x2+10)-4=-x2+6,
易证△PMF∽△QNF,
∴
| PM |
| QN |
| MF |
| FN |
| PF |
| QF |
| 1 |
| 3 |
∴QN=3PM=-3x,NF=3MF=-3x2+18,
∴ON=-3x2+14,
∴Q点坐标为(-3x,3x2-14),
∵Q点在抛物线y=-x2+10上,
∴3x2-14=-9x2+10,
解得:x=-
| 2 |
∴P坐标为(-
| 2 |
| 2 |
∴易得直线PQ为y=2
| 2 |
根据抛物线的对称性可得直线PQ另解为y=-2
| 2 |
点评:本题考查的是二次函数的图象与应用相结合的有关知识,考生要注意的是假设法的求证方法,难度较大.

练习册系列答案
相关题目
 的图象与y轴交于点A,
的图象与y轴交于点A, 的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐
的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐 时x的取值范围。
时x的取值范围。
 中,四边形OABC是矩形,点A,C的坐
中,四边形OABC是矩形,点A,C的坐 =-
=- +
+ 交折线O-A-B于点E.
交折线O-A-B于点E.
