题目内容
2.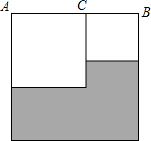 如图,已知线段AB=10cm,点C在线段AB上,分别以AC、BC、AB为边向下作正方形.
如图,已知线段AB=10cm,点C在线段AB上,分别以AC、BC、AB为边向下作正方形.(1)当阴影部分的面积为42cm2时,请求出AC的长;
(2)阴影部分的面积能否为60cm2?如果能,请求出AC的长;如果不能,请说明理由.
分析 (1)设AC的长为xcm,则BC的长为(10-x)cm,根据阴影部分的面积为42cm2列出方程102-x2-(10-x)2=42,解方程即可;
(2)假设阴影部分的面积能为60cm2,设AC的长为ycm,则BC的长为(10-y)cm,根据阴影部分的面积为60cm2列出方程102-y2-(10-y)2=60,解方程即可.
解答 解:(1)设AC的长为xcm,则BC的长为(10-x)cm,
根据题意得:102-x2-(10-x)2=42,
解得x1=3,x2=7.
答:AC的长为3cm或7cm;
(2)假设阴影部分的面积能为60cm2,设AC的长为ycm,则BC的长为(10-y)cm,
根据题意得:102-y2-(10-y)2=60,
整理得:y2-10y+30=0,
∵△=100-4×30=-20<0,
∴方程无实数根,
故阴影部分的面积不能为60cm2.
点评 本题考查了一元二次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.

练习册系列答案
相关题目
13.下列方程是一元二次方程的是( )
| A. | 3x+1=0 | B. | 5x2-6y-3=0 | C. | ax2-x+2=0 | D. | 3x2-2x-1=0 |
10.方程2x2-4=0的解是( )
| A. | x=2 | B. | x=-2 | C. | x=±2 | D. | x=$±\sqrt{2}$ |
7.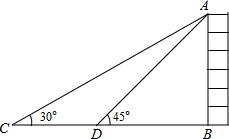 如图,某校数学兴趣小组在大厦前的平地上C处,测得大厦顶端A的仰角∠ACB=30°,在D处测得大厦顶端A的仰角∠ADB=45°,那么从点A观察C、D处的视角∠CAD的度数为( )
如图,某校数学兴趣小组在大厦前的平地上C处,测得大厦顶端A的仰角∠ACB=30°,在D处测得大厦顶端A的仰角∠ADB=45°,那么从点A观察C、D处的视角∠CAD的度数为( )
 如图,某校数学兴趣小组在大厦前的平地上C处,测得大厦顶端A的仰角∠ACB=30°,在D处测得大厦顶端A的仰角∠ADB=45°,那么从点A观察C、D处的视角∠CAD的度数为( )
如图,某校数学兴趣小组在大厦前的平地上C处,测得大厦顶端A的仰角∠ACB=30°,在D处测得大厦顶端A的仰角∠ADB=45°,那么从点A观察C、D处的视角∠CAD的度数为( )| A. | 60° | B. | 45° | C. | 30° | D. | 15° |
14.下列说法错误的是( )
| A. | 0是最小的整数 | B. | 1是最小的正整数 | C. | 0是最小的自然数 | D. | 自然数是非负数 |
12.如果三角形的三边长分别为m-1,m,m+1(m为正数),则m的取值范围是( )
| A. | m>0 | B. | m>-2 | C. | m>2 | D. | m<2 |
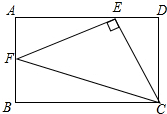 如图,已知矩形ABCD,点E在边AD上,点F在边AB上,CE⊥EF.
如图,已知矩形ABCD,点E在边AD上,点F在边AB上,CE⊥EF.