题目内容
12.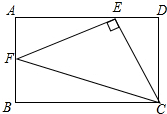 如图,已知矩形ABCD,点E在边AD上,点F在边AB上,CE⊥EF.
如图,已知矩形ABCD,点E在边AD上,点F在边AB上,CE⊥EF.(1)若AB:BC=$\sqrt{3}$:2,请写出图中所有的相似三角形.
(2)若图中所有的三角形都相似,求AB:BC.
分析 (1)由四边形ABCD是矩形,于是得到∠A=∠D=90°,根据CE⊥EF,得到∠AFE=∠DEC,即可得到结论;
(2)由题意得∠AFE=∠BFC=∠EFC=60°,∠FCB=∠ECF=∠ECD=30°,设AF=a,解直角三角形于是得到EF=2a,CF=4a,BC=2$\sqrt{3}$a,即可得到结论.
解答 解:(1)∵四边形ABCD是矩形,
∴∠A=∠D=90°,
∵CE⊥EF,
∴∠AFE+∠AEF=∠AEF+∠DEC=90°,
∴∠AFE=∠DEC,
∴△AEF∽△DCE;
(2)由题意得:∠AFE=∠BFC=∠EFC=60°,∠FCB=∠ECF=∠ECD=30°,
设AF=a,则EF=2a,CF=4a,BC=2$\sqrt{3}$a,
∴AB:BC=3a:2$\sqrt{3}$=3:2$\sqrt{3}$,
∴若图中所有的三角形都相似,AB:BC=3:2$\sqrt{3}$.
点评 本题考查了相似三角形的性质,矩形的性质,熟练掌握各性质定理是解题的关键.

练习册系列答案
 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
12.某批发商欲将一批海产品由A地运往B地,汽车货运公司和铁路货运公司均开办海产品运输业务,已知运输路程为120千米,汽车和火车的速度分别为60千米/时与100千米/时,两货运公司的收费项目及收费标准如下表所示:(元/吨•千米表示每吨货物每千米的运费,元/吨•小时表示每吨货物每小时的冷藏费)
(1)若该批发商待运的海产品有x吨,用式子表示出两种运输方式所花费的费用;
(2)若该批发商待运的海产品有30吨,为节省运费,应选哪种运输方式?
(3)若该批发商待运的海产品有60吨,为节省运费,应选哪种运输方式?
| 运输工具 | 运输费单价元/吨•千米 | 冷藏费单价元/吨•小时 | 过路费/元 | 装卸及管理费/元 |
| 汽车 | 2 | 5 | 200 | 0 |
| 火车 | 1.8 | 5 | 0 | 1600 |
(2)若该批发商待运的海产品有30吨,为节省运费,应选哪种运输方式?
(3)若该批发商待运的海产品有60吨,为节省运费,应选哪种运输方式?

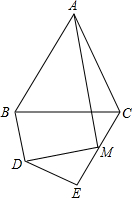 在△ABC中,AB=AC,∠ABC=α,在四边形BDEC中,DB=DE,∠BDE=2α,M为EC的中点,
在△ABC中,AB=AC,∠ABC=α,在四边形BDEC中,DB=DE,∠BDE=2α,M为EC的中点,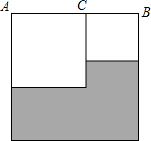 如图,已知线段AB=10cm,点C在线段AB上,分别以AC、BC、AB为边向下作正方形.
如图,已知线段AB=10cm,点C在线段AB上,分别以AC、BC、AB为边向下作正方形.