题目内容
20. 如图,在梯形ABCD中,AD∥BC,AB=AD=DC,AC=BD=BC,试问:图中有多少个黄金三角形,为什么?
如图,在梯形ABCD中,AD∥BC,AB=AD=DC,AC=BD=BC,试问:图中有多少个黄金三角形,为什么?
分析 由等腰梯形的性质和已知条件得出∠ABC=∠DCB,∠ACD=∠ABD=∠ADB=∠DAO=∠BCO=∠CBO,由等腰三角形的性质得出∠BAC=∠ABC=∠DCB=∠BDC,设∠ABD=∠BCO=x,则∠ABC=∠BAC=2x,在△ABC中,由三角形内角和定理得出方程,解方程得出∠BAC=∠ABC=72°,得出△ABC是黄金三角形,同理:△DBC是黄金三角形;由三角形的外角性质得出△ABO是黄金三角形,同理:△DCO是黄金三角形,即可得出结论.
解答 解:图中有4个黄金三角形;理由如下:
∵在梯形ABCD中,AD∥BC,AB=AD=DC,
∴∠ABC=∠DCB,∠ACD=∠ABD=∠ADB=∠DAO=∠BCO=∠CBO,
∵AC=BD=BC,
∴∠BAC=∠ABC=∠DCB=∠BDC,
设∠ABD=∠BCO=x,则∠ABC=∠BAC=2x,
在△ABC中,由三角形内角和定理得:2x+2x+x=180°,
解得:x=36°,
∴∠BAC=∠ABC=72°,
∴△ABC是黄金三角形,
同理:△DBC是黄金三角形;
∵∠AOB=∠DAC+∠ADB=2x=72°=∠BAC,
∴△ABO是黄金三角形,
同理:△DCO是黄金三角形,
∴图中有4个黄金三角形.
点评 本题考查了黄金三角形的定义、等腰梯形的性质、等腰三角形的性质、三角形内角和定理等知识;熟练掌握等腰梯形的性质,由三角形内角和定理得出方程是解决问题的关键.

练习册系列答案
相关题目
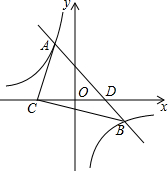 如图,一次函数y=ax+b的图象与反比例函数y=-$\frac{3}{x}$的图象交于A(-1,m)、B(3,n)两点,与x轴交于D点,且C、D两点关于y轴对称.
如图,一次函数y=ax+b的图象与反比例函数y=-$\frac{3}{x}$的图象交于A(-1,m)、B(3,n)两点,与x轴交于D点,且C、D两点关于y轴对称. 由几个小立方体叠成的几何体的主视图和左视图如图所示,求组成几何体的小立方体个数的最大值与最小值,并画出相应的俯视图.
由几个小立方体叠成的几何体的主视图和左视图如图所示,求组成几何体的小立方体个数的最大值与最小值,并画出相应的俯视图.