题目内容
14.设三角形的三边长分别等于下列各组数,能构成直角三角形的是( )| A. | $\sqrt{2}$,$\sqrt{3}$,$\sqrt{5}$ | B. | $\frac{1}{3}$,$\frac{1}{4}$,$\frac{1}{5}$ | C. | $\frac{1}{6}$,$\frac{1}{8}$,$\frac{1}{10}$ | D. | 4,5,6 |
分析 判断是否可以作为直角三角形的三边长,则判断两小边的平方和是否等于最长边的平方即可.
解答 解:A、($\sqrt{2}$)2+($\sqrt{3}$)2=($\sqrt{5}$)2,是直角三角形,故此选项正确;
B、($\frac{1}{4}$)2+($\frac{1}{5}$)2≠($\frac{1}{3}$)2,不是直角三角形,故此选项错误;
C、($\frac{1}{8}$)2+($\frac{1}{10}$)2=($\frac{1}{6}$)2,不是直角三角形,故此选项错误;
D、42+52≠62,不是直角三角形,故此选项错误.
故选:A.
点评 此题主要考查了勾股定理逆定理,关键是掌握勾股定理的逆定理:已知△ABC的三边满足a2+b2=c2,则△ABC是直角三角形.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
4.已知二次函数y=-2(x-3)2+1.下列说法:①其图象的开口向下;②其图象的对称轴为直线x=-3;③其图象顶点坐标为(3,-1);④当x<3时,y随x的增大而增大.其中说法正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
9.下列几组数中不能作为直角三角形三边长度的是( )
| A. | a=7,b=24,c=25 | B. | a=1.5,b=2,c=2.5 | C. | a=$\frac{1}{3}$,b=$\frac{1}{4}$,c=$\frac{1}{5}$ | D. | a=15,b=8,c=17 |
19.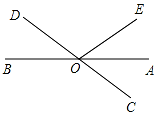 如图,直线AB、CD相交于点O,OA平分∠EOC,∠EOC=70°,则∠BOE的度数等于( )
如图,直线AB、CD相交于点O,OA平分∠EOC,∠EOC=70°,则∠BOE的度数等于( )
 如图,直线AB、CD相交于点O,OA平分∠EOC,∠EOC=70°,则∠BOE的度数等于( )
如图,直线AB、CD相交于点O,OA平分∠EOC,∠EOC=70°,则∠BOE的度数等于( )| A. | 145° | B. | 135° | C. | 35° | D. | 120° |