题目内容
19．
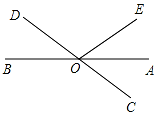如图，直线AB、CD相交于点O，OA平分∠EOC，∠EOC=70°，则∠BOE的度数等于（ ）| A． | 145° | B． | 135° | C． | 35° | D． | 120° |
分析 根据角平分线的性质可得∠EOA的度数，然后根据补角定义可得答案．
解答 解：∵OA平分∠EOC，∠EOC=70°，
∴∠EOA=35°，
∴∠BOE=180°-35°=145°，
故选：A．
点评 此题主要考查了角平分线的定义，以及补角定义，关键是掌握角平分线把角分成相等的两部分．
练习册系列答案
相关题目
9．
如图，AB为⊙O的直径，已知∠ACD=20°，则∠BAD的度数为（ ）
如图，AB为⊙O的直径，已知∠ACD=20°，则∠BAD的度数为（ ）| A． | 40° | B． | 50° | C． | 60° | D． | 70° |
如图，已知⊙A过原点O且与x轴交于点C（6，0），与y轴交于点B（0，8），P为圆上第一象限的点，连结OP，PC，设过点O，C的抛物线的顶点为D，若存在以O，C，D为顶点的三角形与△OCP相似，则P点的坐标为（$\frac{192}{25}$，$\frac{144}{25}$）．
7．（x-a）2的计算结果是（ ）
| A． | x2-2ax+a2 | B． | x2+a2 | C． | x2+2ax+a2 | D． | x2+2ax-a2 |
14．设三角形的三边长分别等于下列各组数，能构成直角三角形的是（ ）
| A． | $\sqrt{2}$，$\sqrt{3}$，$\sqrt{5}$ | B． | $\frac{1}{3}$，$\frac{1}{4}$，$\frac{1}{5}$ | C． | $\frac{1}{6}$，$\frac{1}{8}$，$\frac{1}{10}$ | D． | 4，5，6 |
数a、b在数轴上的位置如图所示，化简：a+|b|-|a|=-b．
11．有一组数据：6，6，5，8，10．它们的中位数是（ ）
| A． | 5 | B． | 8 | C． | 6 | D． | 10 |
8．如（x+m）与（x+4）的乘积中不含x的一次项，则m的值为（ ）
| A． | -4 | B． | 4 | C． | 0 | D． | 1 |
如图，AB=5cm，BC=3cm，如果O是线段AC的中点，求线段OB=1cm．