题目内容
11．
如图，∠DAE是⊙O的内接四边形ABCD的一个外角，且∠DAE=∠DAC．求证：DB=DC．
分析 根据圆内接四边形的任意一个外角等于它的内对角得到∠DAE=∠DCB，由圆周角定理得到∠DAC=∠DBC，等量代换得到∠DCB=∠DBC，根据等腰三角形的性质得到答案．
解答 证明：∵∠DAE是⊙O的内接四边形ABCD的一个外角，
∴∠DAE=∠DCB，又∠DAE=∠DAC，
∴∠DCB=∠DAC，又∠DAC=∠DBC，
∴∠DCB=∠DBC，
∴DB=DC．
点评 本题考查的是圆内接四边形的性质，掌握圆内接四边形的任意一个外角等于它的内对角是解题的关键．
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
相关题目
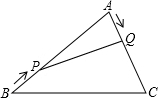如图所示，在△ABC中，AB=18cm，AC=12cm，点P从点B出发以每秒3cm的速度向点A运动，点Q从点A同时出发以每秒2cm的速度向点C运动，其中一个动点到达端点时，另一个动点也随之停止运动．当三角形APQ是等腰三角形时，运动的时间是3.6s．
如图，铁路上A、B两地相距25km，C、D为两村庄，DA⊥AB，CB⊥AB垂足分别为A、B，已知DA=15km，CB=10，现在要在铁路AB上修建一个物流中心E．