��Ŀ����
4����ͼ����ƽ��ֱ������ϵ�У�����ֱ�ǡ�ABC��ֱ�Ƕ���CΪ��-4��0��������Ϊ2�������������Ŷ���C��ת������A��x����Ϸ����ֱ����A����B��x�������ߣ�����ֱ�ΪO1��O2��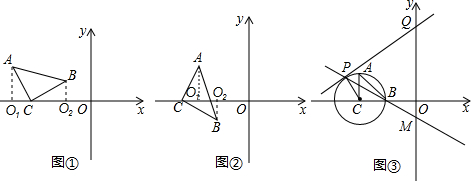
��1����ͼ�ٺ�ͼ��֤���ڵ�B�����������ϵ�����£���ACO1���BCO2ȫ����ѡ������һ��ͼ˵��������ɣ�
��2����ͼ����ʾ����B�˶���x����ʱ����O1��C�غϣ���CΪԲ��CAΪ�뾶��Բ���õ���ͼ��ʾ�ġ�C���ڡ�C����һ������P����P����x���ϣ�������P����C��������y��Ľ���Ϊ��Q��ֱ��BP��y���ڵ�M��
����ͼ������Q��y���������ʱ��д���߶�PQ���߶�QM֮���������ϵ����˵�����ɣ�
�����ŵ�P���˶�����P���������ϳ��⣩���е������߶�֮��Ĺ�ϵ��������˵�����ɣ������䣬����������Сֵ����СֵΪ���٣�
���� ��1��ͼ��������ͬ�ǵ������ȵó���ACO1=��CBO2�����ɵó����ۣ�ͼ��ͬͼ�ٵķ�����֤��
��2�������������ߵ����ʺ�ͬ�ǻ�Ƚǵ������ȵó����ۣ�
�����жϳ�PQ��Сʱ����Q��ԭ��O�������ù��ɶ������PQ����Сֵ��
��� �⣺��1����ACO1���BCO2ȫ��
��ͼ�٣��ߡ�ACB=90�㣬
���ACO1+��BCO2=90�㣬
��AO1��OC��BO2��OC��
���AO1C=��BO2C=90�㣬
���BCO2+��CBO2=90�㣬
���ACO1=��CBO2��
�ڡ�ACO1�͡�CBO2�У�$\left\{\begin{array}{l}{��A{O}_{1}C=��C{O}_{2}B}\\{��AC{O}_{1}=��CB{O}_{2}}\\{AC=BC}\end{array}\right.$��
���ACO1�ա�CBO2��
��ͼ2��ͬ�ٵķ�����֤��
��2���١�PQ�ǡ�C�����ߣ�
���QPC=90�㣬
���QPM+��CPB=90�㣬
��CP=CB��
���CPB=��CBP
���QPM+��CBP=90�㣬
�ߡ�CBP=��OBM��
���QPM+��OBM=90�㣬
�ߡ�OBM+��OMB=90�㣬
���QPM=��OMB��
��QP=QM��
�ڲ��䣬
���ɣ�ͬ��1��
����CQ��
��Rt��CPQ��PQ2=CQ2-CP2
��CP�ǡ�C�İ뾶��
��CPΪ��ֵ��2��
��CQ��Сʱ��PQ��С��
�ߵ�Q��y���ϣ���C��x�ᣬ
���Q�ڵ�O��ʱ��CQ��С����СֵΪCO=4��
��PQ��С=$\sqrt{C{O}^{2}-C{P}^{2}}$=2$\sqrt{3}$��
���� ������Բ���ۺ��⣬��Ҫ������Բ�����ʣ����ߵ����ʣ�ͬ�ǻ�Ƚǵ������ȣ����ɶ������Ȿ��Ĺؼ����жϳ�PQ��Сʱ����Q��λ�ã�

 ���Ͱ�ͨ�������Сѧ��ʱͬ�����ϵ�д�
���Ͱ�ͨ�������Сѧ��ʱͬ�����ϵ�д� ���Ͱ�ͨ������ϵ�д�
���Ͱ�ͨ������ϵ�д� �ٷ�ѧ����ҵ��������ϵ�д�
�ٷ�ѧ����ҵ��������ϵ�д�| A�� | 3m2n3��-m2n3 | B�� | $\frac{xy}{5}$��2xy | C�� | -1��$\frac{��}{4}$ | D�� | a3��x3 |
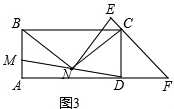
 ��ͼ����֪���κ���ͼ��Ķ�������Ϊ��2��0����ֱ��y=x+1����κ�����ͼ����A��B���㣬���е�A��y���ϣ�
��ͼ����֪���κ���ͼ��Ķ�������Ϊ��2��0����ֱ��y=x+1����κ�����ͼ����A��B���㣬���е�A��y���ϣ�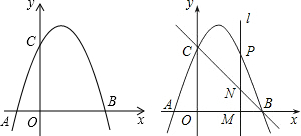
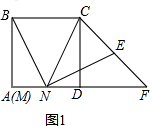
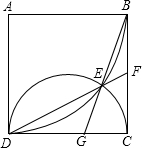 ��ͼ���ڱ߳�Ϊ1��������ABCD�У���AΪԲ�ģ�ABΪ�뾶�Ļ�����DCΪֱ���İ�Բ���ڵ�E������DE���ӳ���BC��F������BE���ӳ���DC��G��
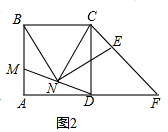
��ͼ���ڱ߳�Ϊ1��������ABCD�У���AΪԲ�ģ�ABΪ�뾶�Ļ�����DCΪֱ���İ�Բ���ڵ�E������DE���ӳ���BC��F������BE���ӳ���DC��G��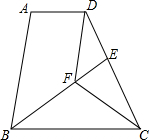 ��֪����ͼ�����ı���ABCD�У�AD��BC��BC=DC��CFƽ�֡�BCD��DF��AB��BF���ӳ��߽�DC�ڵ�E����֤��
��֪����ͼ�����ı���ABCD�У�AD��BC��BC=DC��CFƽ�֡�BCD��DF��AB��BF���ӳ��߽�DC�ڵ�E����֤��