题目内容
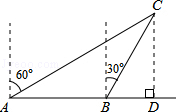 如图,一渔船由西往东航行,在A点测得海岛C位于北偏东40°的方向,前进20海里到达B点,此时,测得海岛C位于北偏东30°的方向,则海岛C到航线AB的距离CD等于
如图,一渔船由西往东航行,在A点测得海岛C位于北偏东40°的方向,前进20海里到达B点,此时,测得海岛C位于北偏东30°的方向,则海岛C到航线AB的距离CD等于考点:解直角三角形的应用-方向角问题
专题:
分析:根据方向角的定义及余角的性质求出∠CAD=30°,∠CBD=60°,再由三角形外角的性质得到∠CAD=30°=∠ACB,根据等角对等边得出AB=BC=20,然后解Rt△BCD,求出CD即可解答.
解答:解:根据题意可知∠CAD=30°,∠CBD=60°,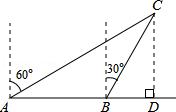
∵∠CBD=∠CAD+∠ACB,
∴∠CAD=30°=∠ACB,
∴AB=BC=20海里,
在Rt△CBD中,∠BDC=90°,∠DBC=60°,sin∠DBC=
,
∴sin60°=
,
∴CD=12×sin60°=20×
=10
海里.
故答案为:10
海里.

∵∠CBD=∠CAD+∠ACB,
∴∠CAD=30°=∠ACB,
∴AB=BC=20海里,
在Rt△CBD中,∠BDC=90°,∠DBC=60°,sin∠DBC=
| CD |
| BC |
∴sin60°=
| CD |
| BC |
∴CD=12×sin60°=20×
| ||
| 2 |
| 3 |
故答案为:10
| 3 |
点评:本题考查了解直角三角形的应用,难度适中.解一般三角形,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
下列图形中,既是轴对称图形又是中心对称图形的是( )
| A、等腰三角形 | B、菱形 |
| C、平行四边形 | D、直角三角形 |
 如图,AB是线段CD的垂直平分线,E,F是AB上的两点,求证:∠ECF=∠EDF.
如图,AB是线段CD的垂直平分线,E,F是AB上的两点,求证:∠ECF=∠EDF.