题目内容
3. 四边形ABCD中,AB=CD,M、N是分别AD、BC的中点,延长BA、MN、CD分别交于点F、E,试说明∠1=∠2.
四边形ABCD中,AB=CD,M、N是分别AD、BC的中点,延长BA、MN、CD分别交于点F、E,试说明∠1=∠2.
分析 连接BD,取BD的中点H,连接HN、HM,根据三角形中位线定理得到∠HMN=∠2,∠HNM=∠1和∠HMN=∠HNM,证明结论.
解答  证明:连接BD,取BD的中点H,连接HN、HM,
证明:连接BD,取BD的中点H,连接HN、HM,
∵M、H是分别BC、BD的中点,
∴MH∥CE,MH=$\frac{1}{2}$CD,
∴∠HMN=∠2,
∵N、H是分别AD、BD的中点,
∴NH∥AB,NH=$\frac{1}{2}$AB,
∴∠HNM=∠1,
∵AB=CD,∴HM=HN,
∴∠HMN=∠HNM,
∴∠1=∠2.
点评 本题考查的是三角形中位线定理,掌握三角形的中位线平行于第三边且等于第三边的一半、正确作出辅助线是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
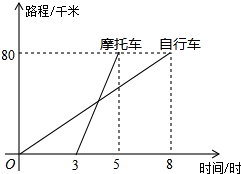 如图表示一骑自行车者和一骑摩托车者沿相同的路线,由甲地到乙地行驶过程中路程和时间之间的关系图,已知两地相距80千米,请根据图象回答:
如图表示一骑自行车者和一骑摩托车者沿相同的路线,由甲地到乙地行驶过程中路程和时间之间的关系图,已知两地相距80千米,请根据图象回答: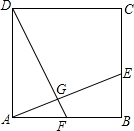 如图,已知点E、F分别为正方形ABCD的边BC、AB上的点,且AF=BE,AE与DF交于点G,试猜想AE与DF之间的大小关系和位置关系,并证明你的猜想.
如图,已知点E、F分别为正方形ABCD的边BC、AB上的点,且AF=BE,AE与DF交于点G,试猜想AE与DF之间的大小关系和位置关系,并证明你的猜想.
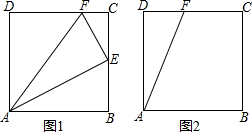
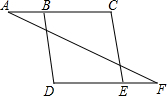 如图,已知∠A=∠F,∠C=∠D,试说明BD∥CE.
如图,已知∠A=∠F,∠C=∠D,试说明BD∥CE.