题目内容
17.若m是非负整数,且关于x的方程(m-1)x2-2x+1=0有两个实数根,求m的值及其对应方程的根.分析 根据关于x的方程(m-1)x2-2x+1=0有两个实数根,得出m-1≠0,且△≥0,求出m的取值范围,再根据m是非负整数,得出m的值,然后分别把m的值代入原方程,得到两个方程,分别求解即可.
解答 解:∵关于x的方程(m-1)x2-2x+1=0有两个实数根,
∴m-1≠0,即m≠1,且△≥0,即△=4-4(m-1)=8-4m≥0,
解得m≤2,
∵m是非负整数,
∴m=0或2,
当m=0,原方程变为:-x2-2x+1=0,解得x1=-1+$\sqrt{2}$,x2=-1-$\sqrt{2}$,
当m=2,原方程变为:x2-2x+1=0,解得x1=x2=1.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)的根的判别式△=b2-4ac.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
相关题目
8.已知a-b=5,则a2-b2-10b+1的值为( )
| A. | 5 | B. | 6 | C. | 25 | D. | 26 |
9.以下关于一元二次方程的根的说法中,正确的是( )
| A. | 方程x2+x-2=0有一根为-1 | |
| B. | 方程x2+x=0有一根为1 | |
| C. | 方程x2+3x-4=0有两个不相等的实数根 | |
| D. | 方程x2+4=0有两个实数根,并且这两根互为相反数 |
6.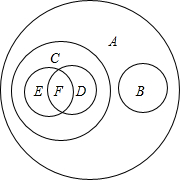 如图为四边形、平行四边形、矩形、正方形、菱形、梯形(B)集合示意图,请将字母所代表的图形分别填入下表:
如图为四边形、平行四边形、矩形、正方形、菱形、梯形(B)集合示意图,请将字母所代表的图形分别填入下表:
 如图为四边形、平行四边形、矩形、正方形、菱形、梯形(B)集合示意图,请将字母所代表的图形分别填入下表:
如图为四边形、平行四边形、矩形、正方形、菱形、梯形(B)集合示意图,请将字母所代表的图形分别填入下表:| A | B | C | D | E | F |
| 四边形 | 梯形 | 平行四边形 | 矩形 | 菱形 | 正方形 |
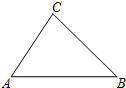 如图,在△ABC中,∠A=60°,∠B=45°,BC=$2\sqrt{2}$,求S△ABC的值.
如图,在△ABC中,∠A=60°,∠B=45°,BC=$2\sqrt{2}$,求S△ABC的值.