题目内容
5.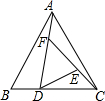 如图,在△ABC中,已知△ABC的面积为1,BD=$\frac{1}{2}$DC,AF=$\frac{1}{2}$FD,CE=$\frac{1}{2}$EF,求△DEF的面积.
如图,在△ABC中,已知△ABC的面积为1,BD=$\frac{1}{2}$DC,AF=$\frac{1}{2}$FD,CE=$\frac{1}{2}$EF,求△DEF的面积.
分析 根据共高的两三角形的面积比等于底边的比分别求出S△ACD、S△CDF、S△DEF,可得答案.
解答 解:∵BD=$\frac{1}{2}$DC,
∴CD=$\frac{2}{3}$BC,
∴S△ACD=$\frac{2}{3}$S△ABC=$\frac{2}{3}$,
又∵AF=$\frac{1}{2}$FD,即DF=$\frac{2}{3}$AD,
∴S△CDF=$\frac{2}{3}$S△ACD=$\frac{4}{9}$,
∵CE=$\frac{1}{2}$EF,即EF=$\frac{2}{3}$CF,
∴S△DEF=$\frac{2}{3}$S△CDF=$\frac{8}{27}$.
点评 本题主要考查三角形的面积,掌握共高的两三角形的面积比等于底边的比是解题的关键.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
17.某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表:
已知日销售量y是售价x的一次函数.
(1)直接写出日销售量y(件)与销售价x(元)的函数关系.
(2)要使每日的销售利润最大,每件产品的售价应定为多少元?此时的日销售利润是多少?若日销售利润低于125元且不亏本,请直接写出售价的取值范围.
| x(元) | 15 | 20 | 30 | … |
| y(件) | 25 | 20 | 10 | … |
(1)直接写出日销售量y(件)与销售价x(元)的函数关系.
(2)要使每日的销售利润最大,每件产品的售价应定为多少元?此时的日销售利润是多少?若日销售利润低于125元且不亏本,请直接写出售价的取值范围.

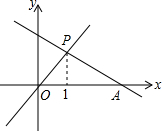 如图,已知一次函数y=kx+b(k,b为常数,且k≠0)的图象与x轴相交于点A(3,0),若正比例函数y=mx(m为常数,且m≠0)的图象与一次函数的图象相交于点P,且点P的横坐标为1,则关于x的不等式(k-m)x+b>0的解集为x<1,关于x的不等式组$\left\{\begin{array}{l}{mx<0}\\{kx-b<0}\end{array}\right.$的解集为-3<x<0.
如图,已知一次函数y=kx+b(k,b为常数,且k≠0)的图象与x轴相交于点A(3,0),若正比例函数y=mx(m为常数,且m≠0)的图象与一次函数的图象相交于点P,且点P的横坐标为1,则关于x的不等式(k-m)x+b>0的解集为x<1,关于x的不等式组$\left\{\begin{array}{l}{mx<0}\\{kx-b<0}\end{array}\right.$的解集为-3<x<0.