题目内容
9.关于分式$\frac{x-5}{{{x^2}-4x+a}}$,有下列说法,错误的有( )个:(1)当x取1时,这个分式有意义,则a≠3;
(2)当x=5时,分式的值一定为零;
(3)若这个分式的值为零,则a≠-5;
(4)当x取任何值时,这个分式一定有意义,则a>4.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 根据分式值为零的条件是分子等于零且分母不等于零,分式有意义的条件是分母不等于零进行分析即可.
解答 解:(1)当x取1时,这个分式有意义,则a≠3,说法正确;
(2)当x=5时,分式的值一定为零,说法错误,当x=5,a≠-5时,分式的值一定为零;
(3)若这个分式的值为零,则a≠-5,说法正确;
(4)当方程x2-4x+a=0中,b2-4ac=16-4a<0时,此方程无实数根,
解得:a>4,即x取任何值时,这个分式一定有意义,说法正确;
故错误的有1个,
故选:B.
点评 此题主要考查了分式有意义的条件和分式值为零的条件,关键是掌握分式值为零的条件是分子等于零且分母不等于零.
注意:“分母不为零”这个条件不能少.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
19.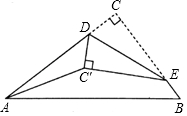 如图,在△ABC中,∠C=90°,AC=4cm,BC=3cm,点D、E分别在AC、BC上.现将△DCE沿DE翻折,使点C落在点C'处.连接AC',则AC'长度的最小值.( )
如图,在△ABC中,∠C=90°,AC=4cm,BC=3cm,点D、E分别在AC、BC上.现将△DCE沿DE翻折,使点C落在点C'处.连接AC',则AC'长度的最小值.( )
 如图,在△ABC中,∠C=90°,AC=4cm,BC=3cm,点D、E分别在AC、BC上.现将△DCE沿DE翻折,使点C落在点C'处.连接AC',则AC'长度的最小值.( )
如图,在△ABC中,∠C=90°,AC=4cm,BC=3cm,点D、E分别在AC、BC上.现将△DCE沿DE翻折,使点C落在点C'处.连接AC',则AC'长度的最小值.( )| A. | 不存在 | B. | 等于1cm | C. | 等于2 cm | D. | 等于2.5 cm |
4.已知-x+y=3,则2(x-y)2-4(x-y)+6的值是( )
| A. | 9 | B. | 12 | C. | -15 | D. | 36 |
19.下列线段中,不可能是同一个三角形的三边上的高的是( )
| A. | 1cm,1cm,2cm | B. | 2cm,2cm,1cm | C. | 2cm,3cm,3cm | D. | 3cm,4cm,6cm |