题目内容
2.已知△ABC≌△DEF,AB=2,AC=4,△DEF的周长为偶数,则EF的长为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 根据全等三角形的性质求出DE和DF,根据三角形三边关系定理求出EF的范围,即可得出答案.
解答 解:∵△ABC≌△DEF,AB=2,AC=4,
∴DE=AB=2,DF=AC=4,
∴4-2<EF<4+2,
∴2<EF<6,
∵△DEF的周长为偶数,
∴EF为4,
故选B.
点评 本题考查了全等三角形的性质和三角形三边关系定理的应用,能熟记全等三角形的性质定理是解此题的关键,注意:全等三角形的对应边相等,对应角相等.

练习册系列答案
相关题目
20.方程$\frac{x-1}{x-2}+\frac{2}{2-x}=2$的解是( )
| A. | x=1 | B. | x=-1 | C. | x=2 | D. | x=-2 |
13.下列命题中,正确的是( )
| A. | 若a•b>0,则a>0,b>0 | B. | 若a•b<0,则a<0,b>0 | ||
| C. | 若a•b=0,则a=0且b=0 | D. | 若a•b=0,则a=0或b=0 |
10. 有理数a,b在数轴上的对应点的位置如图所示:则( )
有理数a,b在数轴上的对应点的位置如图所示:则( )
 有理数a,b在数轴上的对应点的位置如图所示:则( )
有理数a,b在数轴上的对应点的位置如图所示:则( )| A. | a>b | B. | a<b | C. | a<0 | D. | b>0 |
7.如果|a+2|+|b-1|=0,那么(a+b)的值是( )
| A. | -2 | B. | 2 | C. | -1 | D. | 1 |
14. 如图,将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A、B的读数分别为84°、30°,则∠ACB的度数为( )
如图,将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A、B的读数分别为84°、30°,则∠ACB的度数为( )
 如图,将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A、B的读数分别为84°、30°,则∠ACB的度数为( )
如图,将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A、B的读数分别为84°、30°,则∠ACB的度数为( )| A. | 14° | B. | 27° | C. | 28° | D. | 54° |
11.下列说法错误的是( )
| A. | 关于某直线成轴对称的两个图形一定能完全重合 | |
| B. | 线段是轴对称图形 | |
| C. | 全等的两个三角形一定关于某直线成轴对称 | |
| D. | 轴对称图形的对称轴至少有一条 |
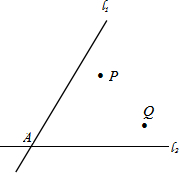 尺规作图:如图,l1、l2交于A点,P、Q的位置如图所示,试确定M点,使它到l1、l2的距离相等,且到P、Q两点的距离也相等.(保留作图痕迹)
尺规作图:如图,l1、l2交于A点,P、Q的位置如图所示,试确定M点,使它到l1、l2的距离相等,且到P、Q两点的距离也相等.(保留作图痕迹)