题目内容
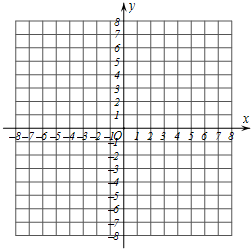 已知,△ABC的三个顶点A,B,C的坐标分别为A(4,0),B(0,-3),C(2,-4).
已知,△ABC的三个顶点A,B,C的坐标分别为A(4,0),B(0,-3),C(2,-4).(1)在如图的平面直角坐标系中画出△ABC,并分别写出点A,B,C关于x轴的对称点A′,B′,C′的坐标;
(2)将△ABC向左平移5个单位,请画出平移后的△A″B″C″,并写出△A″B″C″各个顶点的坐标.
(3)求出(2)中的△ABC在平移过程中所扫过的面积.
考点:作图-平移变换,关于x轴、y轴对称的点的坐标
专题:作图题
分析:(1)根据网格结构找出点A、B、C以及点A′,B′,C′位置,然后顺次连接即可,再根据平面直角坐标系写出各点的坐标;
(2)根据网格结构找出点A、B、C向左平移5个单位的对应点A″、B″、C″,然后顺次连接即可,再根据平面直角坐标系写出各点的坐标;
(3)根据△ABC扫过的面积等于一个平行四边形的面积加上△ABC的面积列式计算即可得解.
(2)根据网格结构找出点A、B、C向左平移5个单位的对应点A″、B″、C″,然后顺次连接即可,再根据平面直角坐标系写出各点的坐标;
(3)根据△ABC扫过的面积等于一个平行四边形的面积加上△ABC的面积列式计算即可得解.
解答: 解:(1)△ABC如图所示,A′(4,0),B′(0,3),C′(2,4);
解:(1)△ABC如图所示,A′(4,0),B′(0,3),C′(2,4);
(2)△A″B″C″如图所示,A″(-1,0),B″(-5,-3),C″(-3,-4);
(3)△ABC在平移过程中所扫过的面积=5×4+(4×4-
×4×3-
×1×2-
×2×4)
=20-(16-6-1-4)
=20-5
=15.
 解:(1)△ABC如图所示,A′(4,0),B′(0,3),C′(2,4);
解:(1)△ABC如图所示,A′(4,0),B′(0,3),C′(2,4);(2)△A″B″C″如图所示,A″(-1,0),B″(-5,-3),C″(-3,-4);
(3)△ABC在平移过程中所扫过的面积=5×4+(4×4-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=20-(16-6-1-4)
=20-5
=15.
点评:本题考查了利用平移变换作图,关于x轴对称点的坐标特征,三角形的面积,熟练掌握网格结构准确找出对应点的位置是解题的关键.

练习册系列答案
相关题目
-
的倒数是( )
| 1 |
| 3 |
| A、3 | ||
B、
| ||
| C、-3 | ||
D、±
|
矩形具有而平行四边形不一定具有的特征是( )
| A、对角线互相平分 |
| B、对角线相等 |
| C、两组对角相等 |
| D、两组对边平行且相等 |
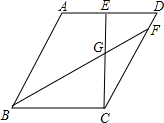 如图,在?ABCD中,CE⊥AD于点E,且CB=CE,点F为CD边上的一点,CB=CF,连接BF交CE于点G.
如图,在?ABCD中,CE⊥AD于点E,且CB=CE,点F为CD边上的一点,CB=CF,连接BF交CE于点G.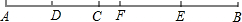
 如图,AB=BC,以AB为直径的⊙O交AC于点D,过点D作DE⊥BC,垂足为E.
如图,AB=BC,以AB为直径的⊙O交AC于点D,过点D作DE⊥BC,垂足为E.