题目内容
如图，某飞机于空中A处探测到目标C，此时飞行高度AC=1200米，从飞机上看地面控制点B
的俯角α=20°（B、C在同一水平线上），求目标C到控制点B的距离（精确到1米）．（参考数据sin20°=0.34，cos20°=0.94，tan20°=0.36）
分析：易知∠B=∠α=20°．在Rt△ABC中，运用正切函数求解．
解答：解：∵AD∥BC，
∴∠B=∠α=20°．
在Rt△ACB中，
∠ACB=90°，tanB=
，
∴BC=
=
=
≈3333（米）．
答：目标C到控制点B的距离为3333米．
∴∠B=∠α=20°．
在Rt△ACB中，
∠ACB=90°，tanB=
| AC |
| BC |
∴BC=
| AC |
| tanB |
| 1200 |
| tan20° |
| 1200 |
| 0.36 |
答：目标C到控制点B的距离为3333米．
点评：本题考查仰角的定义，要求学生能借助仰角构造直角三角形并解直角三角形．
练习册系列答案
阶梯计算系列答案
相关题目
23、如图，某飞机于空中A处探测到目标C，此时飞行高度AC=1200米，从飞机上看到地面控制点B的俯角α=17°，求飞机A到控制点B的距离．（精确到1米）
如图，某飞机于空中A处探测倒地面目标B，此时从飞机上看目标B的俯角α=30°，飞行高度AC=1200米，则飞机到目标B的距离AB为（ ）| A、1200米 | ||
| B、2400米 | ||
C、400
| ||
D、1200
|
数据：sin18°≈0.31，cos18°≈0.95，tan18°≈0.32）
如图，某飞机于空中A处探测得地面目标C，此时飞行高度AC=h米，从飞机上看地面控制点B的俯角为α，那么飞机A到控制点B的距离是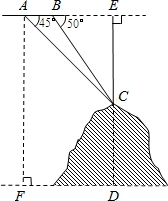
（2013•南通二模）如图，某飞机于空中探测某座山的高度，在点A处飞机的飞行高度是AF=3700米，从飞机上观测山顶目标C的俯角是45°，飞机继续以相同的高度飞行300米到B处，此时观测目标C的俯角是50°，求这座山的高度CD．