题目内容
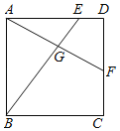
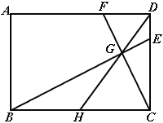
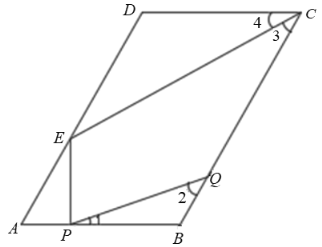
【题目】如图，在平行四边形ABCD中，
，
，AB和CD之间的距离是8，动点P在线段AB上从点A出发沿AB方向以每秒2个单位的速度匀速运动；动点Q在线段BC上从点B出发沿BC的方向以每秒1个单位的速度匀速运动，过点P作
，交线段AD于点E，若
两点同时出发，设运动时间为
秒，
．
（1）当为何值时，BE平分
？
（2）连接PQ,CE，设四边形PECQ的面积为S，求出S与的函数关系式；
（3）是否存在某一时刻，使得
？若存在，请直接给出此时的值（不必写说理过程）；若不存在，请说明理由．
【答案】（1）
；（2）
；（3）存在，
【解析】
（1）过点D作DH⊥AB，过点E作
于点G，证明
求得
，由角平分线的性质可得
，再利用面积法求出
，从而可得方程
，求解即可；
（2）过点Q作
交AB的延长线于点M，延长PE，CD相交于点N，证明
，求得
，求得
，再求得
，
，利用
求解即可；
（3）由
和四边形ABCD是平行四边形可证明
，得
，得出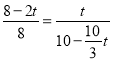
，求解方程即可．
（1）过点D作DH⊥AB，过点E作于点G，
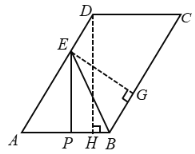
由题意得，
，
在
中，
平分
∵四边形ABCD是平行四边形
∵S四边形ABCD=
即时，BE平分
（2）过点Q作交AB的延长线于点M，延长PE，CD相交于点N，
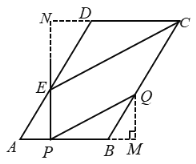
由题意得，
，
由（1）知，
在
中，
∵四边形ABCD是平行四边形
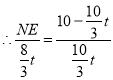
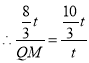
（3）假设存在t使得
由（2）知，，，
，
∵四边形ABCD是平行四边形，
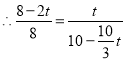
化简得，
解得：
经检验，是原方程的解，符合题意，
即存在t使得CE//QP，此时．
练习册系列答案
发散思维新课堂系列答案
相关题目
