题目内容
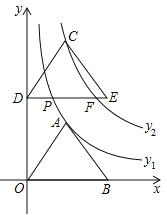
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() 在第一象限,点
在第一象限,点![]() ,
,![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() .把
.把![]() 向上平移
向上平移![]() 个单位长度得到
个单位长度得到![]() .反比例函数
.反比例函数![]() 的图象经过点
的图象经过点![]() ,交
,交![]() 于点
于点![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)设反比例函数![]() 的图象交线段
的图象交线段![]() 于点
于点![]() (点
(点![]() 不与点
不与点![]() 重合) .当
重合) .当![]() 时,请直接写出
时,请直接写出![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)如图,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,由等腰三角形的性质和点B坐标可得OG的长,然后在
,由等腰三角形的性质和点B坐标可得OG的长,然后在![]() 中根据勾股定理可得AG的长,进而可得点A坐标,进一步即可求出k1的值;
中根据勾股定理可得AG的长,进而可得点A坐标,进一步即可求出k1的值;
(2)由题意先用含a的式子表示出点C、F的坐标,然后由点C、F都在![]() 上可得关于a的方程,解方程即得答案;
上可得关于a的方程,解方程即得答案;
(3)分别当出点![]() 与点
与点![]() 重合与
重合与![]() 时a的值,从而可得a的取值范围.
时a的值,从而可得a的取值范围.
解:(1)如图,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,
,

![]() 点
点![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,
 ,
,
![]() 点的坐标为
点的坐标为![]() ,
,
![]() ;
;
(2)由题意得![]() 点的坐标为
点的坐标为![]() ,
,
![]() ,
,
![]() 点的坐标为
点的坐标为![]() ,
,
![]() 点
点![]() 都在反比例函数
都在反比例函数![]() 的图象上,
的图象上,
![]() ,解得
,解得![]() ;
;
(3)当![]() 的顶点
的顶点![]() 落在
落在![]() 上时,点
上时,点![]() 与点
与点![]() 重合,此时,点
重合,此时,点![]() ,
,
![]() ,
,
当![]() 时,∵点P坐标为
时,∵点P坐标为![]() ,
,
∴![]() ,解得:a=2,∴
,解得:a=2,∴![]() ,
,
![]() 当
当![]() 时,
时,![]() 的取值范围是
的取值范围是![]() .
.

【题目】2019年5月,“亚洲文明对话大会”在北京成功举办,某研究机构为了了解10-60岁年年龄段市民对本次大会的关注程度,随机选取了100名年龄在该范围内的市民进行了调查,并将搜集到的数据制成了尚不完整的频数分布表、频数分布直方图和扇形统计图,如下所示:
组别 | 年龄段 | 频数(人数) |
第一组 |
| 5 |
第二组 |
|
|
第三组 |
| 35 |
第四组 |
| 20 |
第五组 |
| 15 |
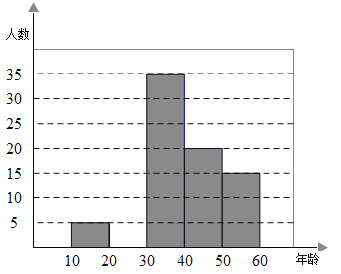

请直接写出第3组人数在扇形统计图中所对应的圆心角是_________度;假设该市现有10-60岁的市民300万人,则40-50岁年龄段的关注本次大会的人数约有___________万人.
【题目】2015年某省为加快建设综合交通体系,对铁路、公路、机场三个重大项目加大建设资金的投入.
(1)机场建设项目中所有6个机场投入的建设资金金额统计如下图,已知机场![]() 投入的建设资金金额是机场
投入的建设资金金额是机场![]() 、
、![]() 所投入建设资金金额之和的三分之二,求机场
所投入建设资金金额之和的三分之二,求机场![]() 投入的建设资金金额是多少亿元?并补全条形统计图.
投入的建设资金金额是多少亿元?并补全条形统计图.
(2)将铁路、公路、机场三项建设所投入的资金金额绘制成如下扇形统计图以及统计表,根据扇形统计图及统计表中的信息,求得![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() .(请直接填写计算结果)
.(请直接填写计算结果)

铁路 | 公路 | 机场 | 铁路、公路、机场三项投入建设资金总金额(亿元) | |
投入资金(亿元) | 300 |
|
|
|
所占百分比 |
| 34% | 6% | |
所占圆心角 |
|
|
|
【题目】为缓解油价上涨给出租车行业带来的成本压力,某市调整出租车运价,调整方案见下列表格及图象(其中![]() 、
、![]() 、
、![]() 为常数):
为常数):
行驶路程 | 收费标准 | |
调价前 | 调价后 | |
不超出 | 起步价9元 | 起步价 |
超出 | 每公里2元 | 每公里 |
超出 | 每公里 | |
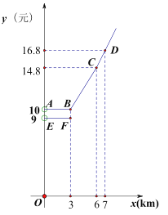
设行驶路程为![]() 时,调价前的运价为
时,调价前的运价为![]() (元),调价后的运价为
(元),调价后的运价为![]() (元).如图,折线
(元).如图,折线![]() 表示
表示![]() 与
与![]() 之间的函数关系;线段
之间的函数关系;线段![]() 表示
表示![]() 时,
时,![]() 与
与![]() 之间的函数关系.根据图表信息,完成下列各题:
之间的函数关系.根据图表信息,完成下列各题:
(1)填空:![]() _____,
_____,![]() _____,
_____,![]() _______;
_______;
(2)写出当![]() 时,
时,![]() 与
与![]() 之间的函数关系式,并在上图中画出该函数图象;
之间的函数关系式,并在上图中画出该函数图象;
(3)当行驶路程为![]() 时,讨论调价前后运价的高低.
时,讨论调价前后运价的高低.
【题目】某学校初二和初三两个年级各有600名同学,为了科普卫生防疫知识,学校组织了一次在线知识竞赛,小宇分别从初二、初三两个年级随机抽取了40名同学的成绩(百分制),并对数据(成绩)进行整理、描述和分析,下面给出了部分信息.
![]() .初二、初三年级学生知识竞赛成绩不完整的频数分布直方图如下(数据分成5组:
.初二、初三年级学生知识竞赛成绩不完整的频数分布直方图如下(数据分成5组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ):
):
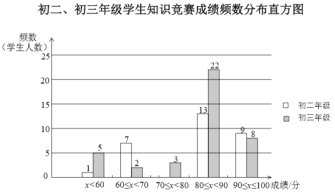
![]() .初二年级学生知识竞赛成绩在
.初二年级学生知识竞赛成绩在![]() 这一组的数据如下:
这一组的数据如下:
80 80 81 83 83 84 84 85 86 87 88 89 89
![]() .初二、初三学生知识竞赛成绩的平均数、中位数、方差如下:
.初二、初三学生知识竞赛成绩的平均数、中位数、方差如下:
平均数 | 中位数 | 方差 | |
初二年级 | 80.8 |
| 96.9 |
初三年级 | 80.6 | 86 | 153.3 |
根据以上信息,回答下列问题:
(1)补全上面的知识竞赛成绩频数分布直方图;
(2)写出表中![]() 的值;
的值;
(3)![]() 同学看到上述的信息后,说自己的成绩能在本年级排在前40%,
同学看到上述的信息后,说自己的成绩能在本年级排在前40%,![]() 同学看到
同学看到![]() 同学的成绩后说:“很遗憾,你的成绩在我们年级进不了前50%”.请判断
同学的成绩后说:“很遗憾,你的成绩在我们年级进不了前50%”.请判断![]() 同学是________(填“初二”或“初三”)年级的学生,你判断的理由是________.
同学是________(填“初二”或“初三”)年级的学生,你判断的理由是________.
(4)若成绩在85分及以上为优秀,请估计初二年级竞赛成绩优秀的人数为____.