题目内容
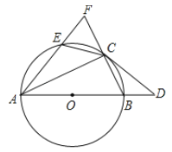
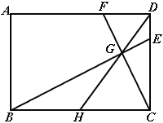
【题目】如图，在矩形ABCD中，点H为边BC的中点，点G为线段DH上一点，且∠BGC=90°，延长BG交CD于点E，延长CG交AD于点F，当CD=4，DE=1时，则DF的长为（ ）
A.2B.
C.
D.
【答案】A
【解析】
延长AD，BE相交于点M，可得△DFG∽△HCG，△DMG∽△HBG，根据相似三角形的性质可得DF=DM，由△MDE∽△CDF可得
，进而得出
，再根据比例的性质解答即可．
解：如图，延长AD，BE相交于点M，
∵DF∥CH，
∴△DFG∽△HCG，
∴ 
，
∵DM∥BH，
∴△DMG∽△HBG，
∴ 
，
∵CH=BH， ∴DF=DM，
又∵矩形
△MDE∽△CDF，
∴ 
∴ 
∴
∴DF＝
．
故选：A．
阅读快车系列答案
【题目】为缓解油价上涨给出租车行业带来的成本压力，某市调整出租车运价，调整方案见下列表格及图象（其中
、
、
为常数）：
行驶路程 | 收费标准 | |
调价前 | 调价后 | |
不超出 | 起步价9元 | 起步价 |
超出 | 每公里2元 | 每公里 |
超出 | 每公里 | |
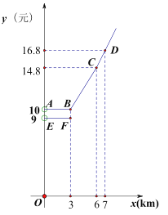
设行驶路程为
时，调价前的运价为
（元），调价后的运价为
（元）．如图，折线
表示与
之间的函数关系；线段
表示
时，与之间的函数关系．根据图表信息，完成下列各题：
（1）填空：
_____，
_____，
_______；
（2）写出当
时，与之间的函数关系式，并在上图中画出该函数图象；
（3）当行驶路程为时，讨论调价前后运价的高低．
【题目】钟南山院士谈到防护新型冠状病毒肺炎时说：“我们需要重视防护，但也不必恐慌，尽量少去人员密集的场所，出门戴口罩，在室内注意通风，勤洗手，多运动，少熬夜．”某学校为了了解学生对新型冠状病毒肺炎防护知识的掌握情况，随机抽取若干名同学利用网络进行了“新冠状病毒肺炎防疫知识”问卷测试．根据测试成绩分布情况，他们将全部测试成绩分成
、
、
、
四组，绘制了如下统计图表：
“新冠状病毒肺炎防疫知识”问卷测试成绩统计表
组别 | 分数/分 | 频数 | 各组总分/分 |
|
| 38 | 2581 |
|
|
| 5543 |
|
| 60 | 5100 |
|
| 30 | 2796 |
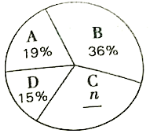
依据以上统计信息，解答下列问题：
（1）求得
，
；
（2）这次测试成绩的中位数落在 组；
（3）求本次全部测试成绩的平均数．
