题目内容
从∠AOB的顶点O引射线OC,使∠AOC:∠BOC=5:4,若∠AOB=27°,求∠AOC的度数.
考点:角的计算
专题:
分析:本题需分类讨论,讨论射线OC在OA,OB之间和不在OA,OB之间两种情况,利用角的和差关系计算即可解题.
解答:解:①射线OC在OA,OB之间,
则∠AOC+∠BOC=27°,
∵∠AOC:∠BOC=5:4,
∴∠AOC=15°,∠BOC=12°;
②射线OC不在OA,OB之间,
则∠AOC-∠BOC=27°,
∵∠AOC:∠BOC=5:4,
∴∠AOC=135°,∠BOC=108°;
则∠AOC+∠BOC=27°,
∵∠AOC:∠BOC=5:4,
∴∠AOC=15°,∠BOC=12°;
②射线OC不在OA,OB之间,
则∠AOC-∠BOC=27°,
∵∠AOC:∠BOC=5:4,
∴∠AOC=135°,∠BOC=108°;
点评:本题考查了角的计算,本题中根据射线OC的位置不同,分类讨论,分别求出∠AOC的度数是解题的关键.

练习册系列答案
相关题目
 如图,矩形草坪的长是80m,宽是10m,现要修建一条平行于草坪边缘的矩形小路,使得小路矩形与草坪矩形相似,求小路的宽.
如图,矩形草坪的长是80m,宽是10m,现要修建一条平行于草坪边缘的矩形小路,使得小路矩形与草坪矩形相似,求小路的宽.
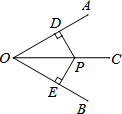 如图,∠AOC=∠BOC,点P在OC上,PD⊥OA于点D,PE⊥OB于点E,若OD=8,OP=10,则PE=
如图,∠AOC=∠BOC,点P在OC上,PD⊥OA于点D,PE⊥OB于点E,若OD=8,OP=10,则PE=