题目内容
如图,△ABC中,AB=AC,D是边BC上一点(不与点B,C重合),以AD为一边作△ADE,使AD=AE,∠BAC=∠DAE,连接CE.
(1)若∠B=45°(如图①),求∠ACE的度数;
(2)设∠BAC=α,∠BCE=β(如图②),试探究点D在线段BC上移动时,α,β之间的数量关系?并说明理由.

(1)若∠B=45°(如图①),求∠ACE的度数;
(2)设∠BAC=α,∠BCE=β(如图②),试探究点D在线段BC上移动时,α,β之间的数量关系?并说明理由.

考点:全等三角形的判定与性质
专题:
分析:(1)根据已知求得∠BAD=∠CAE,然后根据SAS求得三角形全等,进而求得∠B=∠ACE,从而求得∠ACE的度数;
(2)根据三角形的内角和求得∠B+∠ACB=180°一α,根据已知∠ACE+∠ACB=∠BCE=β,由(1)可得∠B=∠ACE,即可求得180°一α=β,进而求得α+β=180°
(2)根据三角形的内角和求得∠B+∠ACB=180°一α,根据已知∠ACE+∠ACB=∠BCE=β,由(1)可得∠B=∠ACE,即可求得180°一α=β,进而求得α+β=180°
解答:解:(1)∵∠BAC=∠DAE,
∴∠BAC一∠DAC=∠DAE一∠DAC
即∠BAD=∠CAE,
在△ABD与△ACE中,
,
∴△ABD≌△ACE (SAS)
∴∠B=∠ACE,
∵∠B=45°,
∴∠ACE=45°.
(2)α+β=180°;
理由:由(1)可知∠B=∠ACE.则∠B+∠ACB=∠ACE+∠ACB,
∵∠B+∠ACB=180°一α,∠ACE+∠ACB=∠BCE=β,
即180°一α=β,
∴α+β=180°.
∴∠BAC一∠DAC=∠DAE一∠DAC
即∠BAD=∠CAE,
在△ABD与△ACE中,
|
∴△ABD≌△ACE (SAS)
∴∠B=∠ACE,
∵∠B=45°,
∴∠ACE=45°.
(2)α+β=180°;
理由:由(1)可知∠B=∠ACE.则∠B+∠ACB=∠ACE+∠ACB,
∵∠B+∠ACB=180°一α,∠ACE+∠ACB=∠BCE=β,
即180°一α=β,
∴α+β=180°.
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
一个宾馆有二人间、三人间、四人间三种客房供游客租住,某旅行团25人准备同时租用这三种客房共9间,如果每个房间都住满,则租房方案共有( )
| A、4种 | B、3种 | C、2种 | D、1种 |
如图,图①、图②、图③分别表示甲、乙、丙三人由A地到B地的路线图(箭头表示行进方向)其中图②中E为AB的中点,图③中AH>BH,我们用a、b、c分别代表三人走过的路程,则a、b、c的大小关系为( )
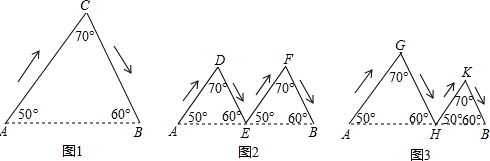

| A、a>b=c |
| B、a<b=c |
| C、a>b>c |
| D、a=b=c |

 如图,A市气象站测得台风中心在A市正东方向160千米的B处,以30千米/时的速度向北偏西60°的BF方向移动,距台风中心100千米范围内是受台风影响的区域.
如图,A市气象站测得台风中心在A市正东方向160千米的B处,以30千米/时的速度向北偏西60°的BF方向移动,距台风中心100千米范围内是受台风影响的区域. 已知∠AOB=30°,P是OA上的一点,OP=4cm,以r为半径作⊙P,若r=
已知∠AOB=30°,P是OA上的一点,OP=4cm,以r为半径作⊙P,若r=