题目内容
1.当n≤0时,关于x的方程(x-p)2+n=0有实数根,其根x为p±$\sqrt{-n}$.分析 先移项得到(x-p)2=-n,利用非负数的性质,当-n≥0,即n≤0,方程有实数解,然后利用直接开平方法解方程.
解答 解:(x-p)2=-n,
当-n≥0,即n≤0,方程有实数解,
所以x-p=±$\sqrt{-n}$,
解得x1=p+$\sqrt{-n}$,x2=p-$\sqrt{-n}$.
故答案为≤0;p±$\sqrt{-n}$.
点评 本题考查了解一元二次方程-直接开平方法:形如x2=p或(nx+m)2=p(p≥0)的一元二次方程可采用直接开平方的方法解一元二次方程.如果方程化成x2=p的形式,那么可得x=±$\sqrt{p}$;如果方程能化成(nx+m)2=p(p≥0)的形式,那么nx+m=±$\sqrt{p}$.

练习册系列答案
相关题目

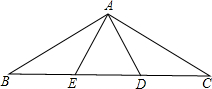 如图,AB=AC,∠BAC=120°,AD⊥AB,AE⊥AC.
如图,AB=AC,∠BAC=120°,AD⊥AB,AE⊥AC. 如图,点P关于OA,OB的对称点分别为C、D,连接CD,交OA于M,交OB于N,若△PMN的周长为10cm,则CD的长为10cm.
如图,点P关于OA,OB的对称点分别为C、D,连接CD,交OA于M,交OB于N,若△PMN的周长为10cm,则CD的长为10cm.