题目内容
1.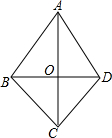 如图,在四边形ABCD中,对角线AC、BD相交于点O,且AB=AD,OB=OD,下列结论:①BC=DC;②AC⊥BD;③AC平分∠BAD;④△AOB≌△COD;⑤∠ABC=∠ADC,其中正确的是①②③⑤(只需填序号).
如图,在四边形ABCD中,对角线AC、BD相交于点O,且AB=AD,OB=OD,下列结论:①BC=DC;②AC⊥BD;③AC平分∠BAD;④△AOB≌△COD;⑤∠ABC=∠ADC,其中正确的是①②③⑤(只需填序号).
分析 先由SSS证明△AOB≌△AOD,得出对应角相等∠AOB=∠AOD,∠BAO=∠DAO,∠ABD=∠ADB,证出AC⊥BD,BC=DC,∠CBD=∠CDB,∠ABC=∠ADC;即可得出结论.
解答 解:在△AOB和△AOD中,$\left\{\begin{array}{l}{AB=AD}&{\;}\\{OB=OD}&{\;}\\{OA=OA}&{\;}\end{array}\right.$,
∴△AOB≌△AOD(SSS),
∴∠AOB=∠AOD,∠BAO=∠DAO,∠ABD=∠ADB,
∵∠AOB+∠AOD=180°,
∴∠AOB=∠AOD=90°,
∴AC⊥BD,
∵OB=OD,
∴BC=DC,
∴∠CBD=∠CDB,
∴∠ABC=∠ADC,
∴①②③⑤正确,④不正确;
故答案为:①②③⑤.
点评 本题考查了全等三角形的判定与性质以及线段垂直平分线的性质;熟练掌握全等三角形的判定方法,证明三角形全等是即为的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.10的平方根是( )
| A. | ±$\sqrt{10}$ | B. | ±$\sqrt{5}$ | C. | ±5 | D. | 5 |
10.下列图形中,既是轴对称图形又是中心对称图形的有( )


| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
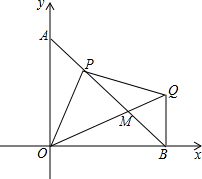 已知:如图,A、B两点坐标为(0,4),B(4,0),P为线段AB上的任一点,过P作OP的垂线与过B点的x轴的垂线交于点Q,OQ与直线AB交于点M.请探究解答下列问题:
已知:如图,A、B两点坐标为(0,4),B(4,0),P为线段AB上的任一点,过P作OP的垂线与过B点的x轴的垂线交于点Q,OQ与直线AB交于点M.请探究解答下列问题: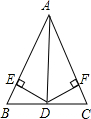 如图,在△ABC中,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,BD=DC,求证:∠B=∠C.
如图,在△ABC中,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,BD=DC,求证:∠B=∠C.