题目内容
11.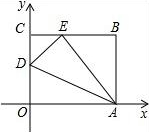 如图,0ABC是一张放在平面直角坐系中的长方形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处.
如图,0ABC是一张放在平面直角坐系中的长方形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处.(1)求D、E两点的坐标;
(2)连接OE交AD于点F,求点F的坐标.
分析 (1)在△EAB中,利用勾股定理求得EB的长,从而得到CE的长,然后在△CDE中依据勾股定理求得CD的长;
(2)由翻折的性质可知点F为OE的中点,从而可求得点F的坐标.
解答 解:(1)由翻折的性质可知:DE=DO,AO=EA.
在Rt△BEA中,BE=$\sqrt{A{E}^{2}-A{B}^{2}}$=6,
∵CE=BC-BE=10-6=4.
∴点E的坐标为(4,8).
设DC的长为x,则DE=OD=8-x.
在Rt△CDE中,DC2+CE2=DE2,即x2+42=(8-x)2,
解得:x=3.
∴OD=8-3=5.
∴点D的坐标为(0,5).
(2)∵点O与点E关于AD对称,
∴点F是OE的中点.
∴点F的坐标为(2,4).
点评 本题主要考查的是翻折的性质、勾股定理的应用,掌握翻折的性质是解题的关键.

练习册系列答案
相关题目
19.在一块直角三角形空地上挖一个矩形水池,要求矩形水池的两条边在直角三角形空地的直角边上.若测得直角三角形空地的一条直角边长为60m,斜边长为100m,则水池的最大面积是( )
| A. | 1200m2 | B. | 1300m2 | C. | 1600m2 | D. | 1140m2 |
16.2010个同学站成一排报数,报到奇数的退出,偶数的留下,留下的同学位置不动重新报数,报到奇数的退出,偶数的留下,…,如此继续,最后留下一个同学,则最后留下的这个同学第一次站的位置是第( )
| A. | 256个 | B. | 512个 | C. | 1024个 | D. | 2010个 |
 如图,在点数是2~7的6张同花色扑克牌中,有2张正面朝上,其余的都是背面朝上,某学生从背面朝上的牌中任意抽取1张牌,其点数恰好在2张正面朝上的牌的点数之间的概率是$\frac{3}{4}$.
如图,在点数是2~7的6张同花色扑克牌中,有2张正面朝上,其余的都是背面朝上,某学生从背面朝上的牌中任意抽取1张牌,其点数恰好在2张正面朝上的牌的点数之间的概率是$\frac{3}{4}$. 观察下列数串排列成的表.从表中可以看到,第2行自左向右第三个数是7,第3行自左向右第二个数是11,第99行自左向右第二个数是387,-1000是第249行自左向右第4个数.
观察下列数串排列成的表.从表中可以看到,第2行自左向右第三个数是7,第3行自左向右第二个数是11,第99行自左向右第二个数是387,-1000是第249行自左向右第4个数.