题目内容
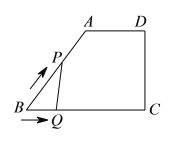
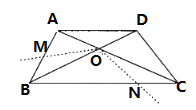
【题目】如图，四边形ABCD中，AD∥BC，AB＝CD，BD平分∠ABC，BD⊥DC．
（1）求出sin∠DBC的值；
（2）若AD=2，把∠BOC绕点O顺时针旋转
（
），交AB于点M，交BC于点N（如图），求证：四边形OMBN的面积为一个定值，并求出这个定值．
【答案】（1）
；（2）
【解析】
（1）设
，根据题意可得
，根据BD⊥DC可列出关于x的方程，即可求解；
（2）根据AD∥BC，推出
，再结合BD平分∠ABC，即可得到
，AB=AD，根据旋转性质得到
从而证的
，从而证的
.
（1）设，
∵AB＝CD，
∴∠ABC=∠BCD，
∵BD平分∠ABC，
∴
，
∴∠BCD=2∠CBD=2x，
，
，
解得：
．
；
（2）证明：
，
，
．
，
在△ONC和△OMB中，
，
．
∴
，
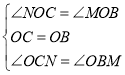由（1）可知，∠CBD=30°，
∴∠ACB=∠ACD=30°，
∴
，
即四边形OMBN的面积为一个定值，这个定值为．
练习册系列答案
王后雄学案教材完全解读系列答案
海淀课时新作业金榜卷系列答案
相关题目
