Question

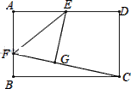
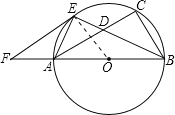
【题目】如图，已知以的边为直径作的外接圆的平分线交于，交于，过作交的延长线于．

（1）求证：是切线；

（2）若求的长．

Answer 1

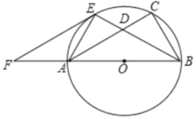
【答案】（1）见详解；（2）

【解析】

（1）要证EF是 的切线，只要连接OE，再证∠FEO=90°即可；
（2）证明△FEA∽△FBE，得出，从而得到AF的值，进而得到，结合勾股定理得到关于AE的方程，即可求出AE的长．

（1）连接OE，

∵∠B的平分线BE交AC于D，

∴∠CBE=∠OBE，

∵EF∥AC，

∴∠CAE=∠FEA，

∵∠OBE=∠OEB，∠CBE=∠CAE，

∴∠FEA=∠OEB，

∵AB是的直径，

∴∠AEB=90°，

∴∠FEO=90°，

∴EF是切线；

（2）∵∠FEA=∠OEB=∠OBE，∠F=∠F，

∴FEA~FBE，

∴，

即：，

∴AF×(AF+15)=10×10，解得：AF=5或AF=-20（舍去），

∴，

∵在RtABE中，AE2+BE2=AB2，

∴AE2+（2AE）2=152，

∴AE=．