题目内容
2.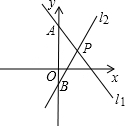 如图,直线l1:y=kx+b与y轴交于点A(0,7),直线l2:y=3x-3交y轴于点B,交直线l1于点P(2,m).
如图,直线l1:y=kx+b与y轴交于点A(0,7),直线l2:y=3x-3交y轴于点B,交直线l1于点P(2,m).(l)求直线l1的解析式;
(2)求△PAB的面积.
分析 (1)先根据点P(2,m)在直线y=3x-3上求得点P的坐标,再利用A、P的坐标待定系数法即可求得直线l1的解析式;
(2)先求得直线y=3x-3与y轴的交点B的坐标,再根据三角形的面积公式即可得.
解答 解:(1)将点P(2,m)代入y=3x-3,
得:m=3,
∴点P的坐标为(2,3),
将点A(0,7)、P(2,3)代入y=kx+b,
得:$\left\{\begin{array}{l}{b=7}\\{2k+b=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-2}\\{b=7}\end{array}\right.$,
∴直线l1的解析式为y=-2x+7;
(2)在y=3x-3中当x=0时,y=-3,
∴点B(0,-3),
则△PAB的面积为$\frac{1}{2}$×10×2=10.
点评 本题主要考查两直线相交或平行问题,熟练掌握两直线的交点坐标满足每一个直线解析式及待定系数法求函数解析式是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12. 如图,a∥b,直线AB分别交a、b于A、B两点,点C在直线b上,且∠1=∠2,则下列结论正确的是( )
如图,a∥b,直线AB分别交a、b于A、B两点,点C在直线b上,且∠1=∠2,则下列结论正确的是( )
 如图,a∥b,直线AB分别交a、b于A、B两点,点C在直线b上,且∠1=∠2,则下列结论正确的是( )
如图,a∥b,直线AB分别交a、b于A、B两点,点C在直线b上,且∠1=∠2,则下列结论正确的是( )| A. | ∠1=∠ABC | B. | ∠1=∠ACB | C. | ∠ABC=∠ACB | D. | ∠2=∠ABC |
13.下列数学符号中,属于中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
10.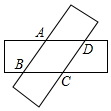 如图,两张等宽的纸条交叉重叠在一起,重叠的部分为四边形ABCD,若测得点A,C之间的距离为6cm,点B,D之间的距离为8cm,则线段AB的长为( )
如图,两张等宽的纸条交叉重叠在一起,重叠的部分为四边形ABCD,若测得点A,C之间的距离为6cm,点B,D之间的距离为8cm,则线段AB的长为( )
 如图,两张等宽的纸条交叉重叠在一起,重叠的部分为四边形ABCD,若测得点A,C之间的距离为6cm,点B,D之间的距离为8cm,则线段AB的长为( )
如图,两张等宽的纸条交叉重叠在一起,重叠的部分为四边形ABCD,若测得点A,C之间的距离为6cm,点B,D之间的距离为8cm,则线段AB的长为( )| A. | 5cm | B. | 4.8cm | C. | 4.6cm | D. | 4cm |
17. 如图所示,添加一个条件后可得AB∥CD,则添加这个条件不能是( )
如图所示,添加一个条件后可得AB∥CD,则添加这个条件不能是( )
 如图所示,添加一个条件后可得AB∥CD,则添加这个条件不能是( )
如图所示,添加一个条件后可得AB∥CD,则添加这个条件不能是( )| A. | ∠A=∠2 | B. | ∠A=∠1 | C. | ∠B=∠2 | D. | ∠A+∠ACD=180° |
14.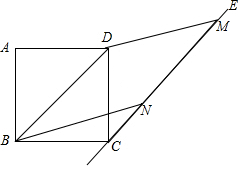 已知正方形ABCD中,过点C作直线CE,使CE∥BD;以BD为一边作?BDMN,且顶点M,N均在直线CE上,给出下列结论:
已知正方形ABCD中,过点C作直线CE,使CE∥BD;以BD为一边作?BDMN,且顶点M,N均在直线CE上,给出下列结论:
①S平行四边形BDMN=S正方形ABCD;②当四边形BDMN菱形时,∠NBC=15°或165°.则下列说法正确的是( )
 已知正方形ABCD中,过点C作直线CE,使CE∥BD;以BD为一边作?BDMN,且顶点M,N均在直线CE上,给出下列结论:
已知正方形ABCD中,过点C作直线CE,使CE∥BD;以BD为一边作?BDMN,且顶点M,N均在直线CE上,给出下列结论:①S平行四边形BDMN=S正方形ABCD;②当四边形BDMN菱形时,∠NBC=15°或165°.则下列说法正确的是( )
| A. | ①②都对 | B. | ①②都错 | C. | ①对②错 | D. | ①错②对 |
11.2017年亚冬会速滑比赛的10名运动员的身高如表:
则该10名运动员身高的平均数和中位数分别是( )
| 身高(cm) | 170 | 172 | 180 | 183 |
| 人数(个) | 3 | 2 | 3 | 2 |
| A. | 176cm,178cm | B. | 176cm,176cm | C. | 175cm,176cm | D. | 175cm,178cm |