题目内容
15.解方程:①x2-2x=3
②2(x-1)2=6
③3x2-2=2x
④5x(3x+2)=4(3x+2)
⑤4x2-6x-2=2x+1
⑥(3x-11)(x-2)=2.
分析 ①④⑥利用分解因式法解方程即可;
②利用直接开平方法解方程;
③⑤整理成一般形式,利用公式法解方程即可.
解答 解:①x2-2x=3
x2-2x-3=0
(x-3)(x+1)=0
x-3=0,x+1=0
解得:x1=3,x2=-1.
②2(x-1)2=6
(x-1)2=3
x-1=±$\sqrt{3}$
解得:x1=1+$\sqrt{3}$,x2=1-$\sqrt{3}$.
③3x2-2=2x
3x2-2x-2=0
a=1,b=-2,c=-2
b2-4ac=(-2)2-4×3×(-2)=28
x=$\frac{2±2\sqrt{7}}{6}$
解得:x1=$\frac{1+\sqrt{7}}{3}$,x2=$\frac{1-\sqrt{7}}{3}$.
④5x(3x+2)=4(3x+2)
5x(3x+2)-4(3x+2)=0
(3x+2)(5x-4)=0
3x+2=0,5x-4=0
解得:x1=-$\frac{3}{2}$,x2=$\frac{4}{5}$.
⑤4x2-6x-2=2x+1
4x2-8x-3=0
a=4,b=-8,c=-3
b2-4ac=(-8)2-4×4×(-3)=112
x=$\frac{8±4\sqrt{7}}{8}$
解得:x1=$\frac{2+\sqrt{7}}{2}$,x2=$\frac{2-\sqrt{7}}{2}$.
⑥(3x-11)(x-2)=2
3x-17x+20=0,
(3x-5)(x-4)=0
解得:x1=$\frac{5}{3}$,x2=4.
点评 此题考查解一元二次方程,根据方程的特点,灵活选用适当的方法解方程即可.

练习册系列答案
相关题目
5.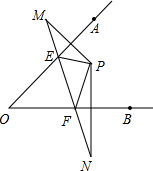 如图所示.点P在∠AOB的内部,点M、N分别是点P关于直线OA、OB的对称点,线段MN交OA、OB于点E、F.
如图所示.点P在∠AOB的内部,点M、N分别是点P关于直线OA、OB的对称点,线段MN交OA、OB于点E、F.
(1)若MN=20cm,求△PEF的周长.
(2)若∠AOB=35°,求∠EPF的度数.
 如图所示.点P在∠AOB的内部,点M、N分别是点P关于直线OA、OB的对称点,线段MN交OA、OB于点E、F.
如图所示.点P在∠AOB的内部,点M、N分别是点P关于直线OA、OB的对称点,线段MN交OA、OB于点E、F.(1)若MN=20cm,求△PEF的周长.
(2)若∠AOB=35°,求∠EPF的度数.
10.关于x的方程(a-2)x2+x+2a=0是一元二次方程的条件是( )
| A. | a≠0 | B. | a≠2 | C. | a≠$\sqrt{2}$ | D. | a≠-3 |