题目内容
一个正多边形的每个外角都等于60°，则它是 边形，内角和是 度．
考点：多边形内角与外角
专题：
分析：根据任何多边形的外角和都是360°，利用360除以外角的度数就可以求出多边形的边数；n边形的内角和是（n-2）•180°，把多边形的边数代入公式，就得到多边形的内角和．
解答：解：360÷60=6，则它是六边形；
内角和是：（6-2）•180°=720度．
故答案为：六，720．
内角和是：（6-2）•180°=720度．
故答案为：六，720．
点评：本题考查了多边形内角与外角，根据外角和的大小与多边形的边数无关，由外角和求正多边形的边数，是常见的题目，需要熟练掌握．
练习册系列答案
相关题目
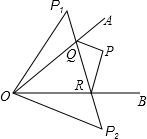如图所示，∠AOB=45°，角内有一点P，P1、P2分别是点P关于两边OA和OB的对称点，连P1P2与角两边交于Q、R．
操作：剪若干个大小形状完全相同的直角三角形，三边长分别记为a、b、c（如图①），分别用4张这样的直角三角形纸片拼成如图②③的形状，图②中的两个小正方形的面积S2、S3与图③中小正方形的面积S1有什么关系？你能得到a、b、c之间有什么关系？在数0、0.
、
、
、0.1010010001…、
、
中，无理数有（ ）
| • |
| 2 |
| -π |
| 3 |
| 22 |
| 7 |
| 131 |
| 11 |
| 27 |
| A、1个 | B、2个 | C、3个 | D、4个 |