题目内容
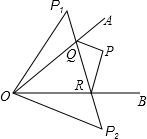 如图所示,∠AOB=45°,角内有一点P,P1、P2分别是点P关于两边OA和OB的对称点,连P1P2与角两边交于Q、R.
如图所示,∠AOB=45°,角内有一点P,P1、P2分别是点P关于两边OA和OB的对称点,连P1P2与角两边交于Q、R.(1)当P1P2=20cm时,△PQR的周长=
(2)连接OP1、OP2,则△OP1P2为
(3)求∠QPR的度数.
考点:轴对称的性质
专题:
分析:(1)根据轴对称的性质可得PQ=P1Q,PR=P2R,然后求出△PQR的周长=P1P2;
(2)连接OP,根据轴对称的性质可得OP1=OP=OP2,∠AOP1=AOP,∠BOP2=∠BOP,再求出∠P1OP2=2∠AOB=90°,再根据等腰直角三角形的定义判定即可;
(3)根据轴对称的性质可得∠OPQ=∠P1,∠OPR=∠P2,然后求解即可.
(2)连接OP,根据轴对称的性质可得OP1=OP=OP2,∠AOP1=AOP,∠BOP2=∠BOP,再求出∠P1OP2=2∠AOB=90°,再根据等腰直角三角形的定义判定即可;
(3)根据轴对称的性质可得∠OPQ=∠P1,∠OPR=∠P2,然后求解即可.
解答: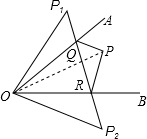 解:(1)∵P1、P2分别是点P关于两边OA和OB的对称点,
解:(1)∵P1、P2分别是点P关于两边OA和OB的对称点,
∴PQ=P1Q,PR=P2R,
∴△PQR的周长=P1P2=20cm;
(2)如图,连接OP,
由轴对称的性质得,OP1=OP=OP2,∠AOP1=AOP,∠BOP2=∠BOP,
所以,∠P1OP2=2∠AOB=90°,
∴△OP1P2为等腰直角三角形;
(3)∵∠P1OP2=90°,
∴∠P1+∠P2=90°,
由轴对称的性质得,∠OPQ=∠P1,∠OPR=∠P2,
∴∠QPR=∠OPQ+∠OPR=90°.
故答案为:(1)20;(2)等腰直角.
 解:(1)∵P1、P2分别是点P关于两边OA和OB的对称点,
解:(1)∵P1、P2分别是点P关于两边OA和OB的对称点,∴PQ=P1Q,PR=P2R,
∴△PQR的周长=P1P2=20cm;
(2)如图,连接OP,
由轴对称的性质得,OP1=OP=OP2,∠AOP1=AOP,∠BOP2=∠BOP,
所以,∠P1OP2=2∠AOB=90°,
∴△OP1P2为等腰直角三角形;
(3)∵∠P1OP2=90°,
∴∠P1+∠P2=90°,
由轴对称的性质得,∠OPQ=∠P1,∠OPR=∠P2,
∴∠QPR=∠OPQ+∠OPR=90°.
故答案为:(1)20;(2)等腰直角.
点评:本题考查了轴对称的性质,等腰直角三角形的判定,熟记性质是解题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
下列叙述中,错误的是( )
| A、-2y的系数是-2,次数是1 |
| B、单项式ab2的系数是1,次数是2 |
| C、2x-3是一次二项式 |
| D、3x2+xy-4是二次三项式 |
 如图,在正方形ABCD中,E、F分别为BC、AB上的点,且∠FED=90°,∠DFE=60°,若正方形边长为1,求△DEF的面积.
如图,在正方形ABCD中,E、F分别为BC、AB上的点,且∠FED=90°,∠DFE=60°,若正方形边长为1,求△DEF的面积. 在一边靠墙的空地上,用砖墙围成三格的矩形场地,已知砖墙在地面上占地总长度160m,问分隔墙在地面上的长度x为多少时所围场地总面积最大?并求这个最大面积.
在一边靠墙的空地上,用砖墙围成三格的矩形场地,已知砖墙在地面上占地总长度160m,问分隔墙在地面上的长度x为多少时所围场地总面积最大?并求这个最大面积.